Однородные системы линейных уравнений

Пусть дана однородная система

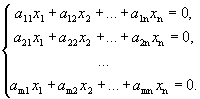(1)

Рассмотрим соответствующую неоднородную систему

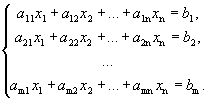(2)

С помощью матриц

, , ,

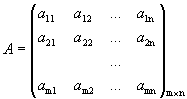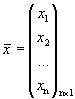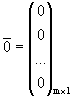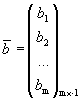
эти системы можно записать в матричном виде.

. (3)

. (4)

Справедливы следующие свойства решений однородной и неоднородной систем.

Теорема 1. Линейная комбинация решений однородной системы (1) является решением системы (1).

Доказательство. Пусть , и - решения однородной системы (1). Рассмотрим , где , и - некоторые произвольные числа. Так как , и являются решениями, то , и . Найдем .

.

является решением системы (1).

Теорема 2. Разность двух решений неоднородной системы (2) является решением однородной системы (1).

Доказательство. Пусть и - решения системы (2). Рассмотрим .

, .

.

является решением однородной системы (1).

Теорема 3. Сумма решения однородной системы (1) с решением неоднородной системы (8.2) есть решение неоднородной системы (2).

Пусть- решение системы (1), - решение системы (2). Покажем, что - решение системы (2).

Доказательство. , .

.

является решением неоднородной системы (2).