Линейное векторное пространство

Определение 1. Упорядоченная совокупность из n действительных чисел (а₁, а₂, …, а_n) называется n-мерным вектором ā(а₁, а₂, …, а_n). Числа а₁, а₂, ..., а_n называются координатами вектора.

Два n-мерных вектора (а₁, а₂, …, а_n) и (b₁, b₂, …, b_n) считаются равными, если равны их соответствующие координаты:

, ().

Вектор, все координаты которого равны нулю, называется ноль-вектором и обозначается .

Пример. (3; 1/2; 0,7; -2; 0) - пятимерный вектор.

Определение 2. Суммой (разностью) двух n-мерных векторов (а₁, а₂, …, а_n) и (b₁, b₂, …, b_n) называется n-мерный вектор, координаты которого равны суммам (разностям) соответствующих координат исходных векторов:

=(a₁b₁; a₂b₂; …; a_nb_n).

Определение 3. Произведением n-мерного вектора (а₁, а₂, …, а_n) на число k называется n‑мерный вектор, координаты которого равны произведениям координат вектора на число k:

k · =(ka₁; ka₂; …; ka_n).

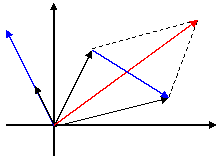
Для геометрических векторов (n<4) эти операции эквивалентны правилу параллелограмма или треугольника и растяжению (сжатию) вектора.

Пример. Пусть даны три вектора: , и (-1,2).

+ = (5; 4), - = (3; -2), 2=(-2,4).

Y

2 +

-

0 X

Свойства операций над векторами:

1) +=+ - коммутативность,

2) +(+)=(+)+ - ассоциативность,

3) k·()=k·k· - дистрибутивность,

4) (k₁k₂)·= k_{1 ·} k₂·,

5) (k₁·k₂)·=k₁·(k₂·),

6) 1·=,

7) 0·=,

8) k·=,

9) k·=.

Определение 4. Совокупность всех n-мерных векторов с введенными на ней операциями сложения и умножения на число называется n-мерным линейным векторным пространством и обозначается Eⁿ.

Пример. E² - совокупность всех двухмерных векторов плоскости с обычными операциями сложения и умножения на число.