Системы линейных уравнений

Определение 1. Система вида

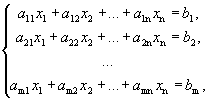
называется системой m линейных уравнений с n неизвестными, где x₁, x₂, …, x_n - неизвестные, a_ij, i=, j= - коэффициенты при неизвестных, b₁, b₂, …, b_m - свободные члены.

Определение 2. Если все свободные члены равны нулю, то система называется однородной, и неоднородной - в противном случае.

Определение 3. Решением системы называется совокупность из n чисел с₁, с₂, …, с_n, при подстановке которой в систему вместо неизвестных будет получено m числовых тождеств.

Определение 4. Система называется совместной, если она имеет хотя бы одно решение, и несовместной в противном случае.

Определение 5. Совместная система называется определенной, если она имеет единственное решение, и неопределенной - в противном случае.

При изучении систем исследуют три вопроса:

1) совместна система или нет;

2) если система совместна, то является ли она определенной или неопределенной;

3) нахождение единственного решения в случае определенной системы и всех решений в случае неопределенной.