Элементарные преобразования

над матрицей. Нахождение обратной матрицы

Определение 1. Элементарными преобразованиями над матрицей называются:

1) умножение любой строки на число, отличное от нуля;

2) прибавление к элементам одной строки соответствующих элементов другой, умноженных на одно и то же число;

3) перестановка строк;

4) отбрасывание строки из нулей.

Определение 2. Две матрицы называются эквивалентными (А~В), если от одной можно перейти к другой с помощью конечного числа элементарных преобразований.

Теорема. Любую невырожденную квадратную матрицу с помощью элементарных преобразований можно привести к единичной матрице того же порядка. Применяя ту же последовательность элементарных преобразований к единичной матрице, можно получить обратную матрицу к данной.

Обычно элементарные преобразования производят над данной матрицей и единичной одновременно. Для этого составляют расширенную матрицу, в левой части которой стоит исходная матрица, а в правой - единичная матрица того же порядка. С помощью элементарных преобразований в левой части создают единичную матрицу, параллельно в правой части автоматически создается обратная матрица.

.

Пример. Пусть дана матрица .

Составим расширенную матрицу:

~~~~.

, .
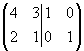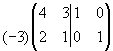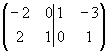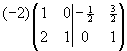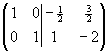
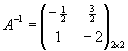