Определители

Пусть дана квадратная матрица порядка n:

А = .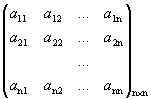

Определение 1. Определителем n-го порядка матрицы А называется число, равное алгебраической сумме n! слагаемых, каждое из которых равно произведению n элементов матрицы А , взятых по одному из каждой строки и каждого столбца, причем каждое слагаемое берется со знаком "+" или "-".

.

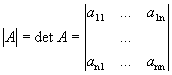Пример 1. Определитель второго порядка. n=2, 2!=1 · 2=2 слагаемых.

.

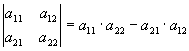Мнемоническое правило вычисления определителя второго порядка:

слагаемое со знаком "-", слагаемое со знаком "+".

Пример 2. Определитель третьего порядка. n=3, 3!=1 · 2 · 3=6 слагаемых,

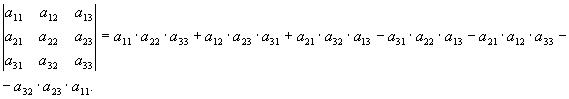
Мнемоническое правило вычисления определителя третьего порядка:

слагаемые со знаком "+", слагаемые со знаком "-".

Можно построить мнемонические правила для вычисления определителей порядка выше чем три, но они будут слишком громоздкими. Поэтому вычисление таких определителей основано на свойствах определителей.