Операции над матрицами

Определение 1. Транспонированием матрицы называется такое преобразование матрицы, при котором строки и столбцы меняются ролями при сохранении номеров. Транспонированная матрица обозначается А^Т.

, , .

Для квадратной матрицы это преобразование эквивалентно симметричному отображению относительно главной диагонали.

Определение 2. Суммой (разностью) двух матриц одинакового порядка называется матрица того же порядка, каждый элемент которой равен сумме (разности) соответствующих элементов исходных матриц.

, , .

Определение 3. Произведением матрицы на число называется матрица того же размера, каждый элемент которой равен произведению соответствующего элемента исходной матрицы на это число.

, , .

Пример. , ,

, ,

, .

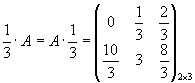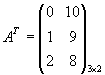Определение 4. Произведением двух матриц А и В, размеры которых заданы соотношением: количество столбцов первой матрицы равно количеству строк второй, называется матрица С, у которой количество строк равно количеству строк первой матрицы, а количество столбцов равно количеству столбцов второй. Каждый элемент данной матрицы равен сумме попарных произведений элементов соответствующей строки первой матрицы и элементов соответствующего столбца второй.

, , , .

Примеры. 1) , ,

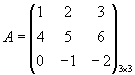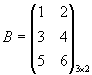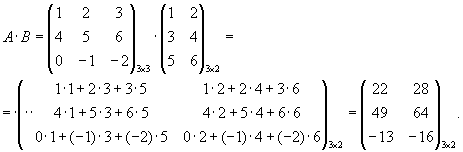
Умножить В на А нельзя, так как число столбцов матрицы В не равно числу строк матрицы А.

Пример 2. , ,

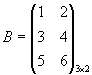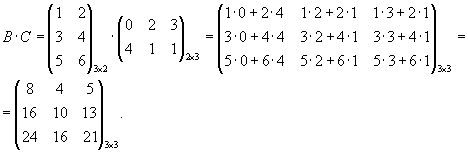
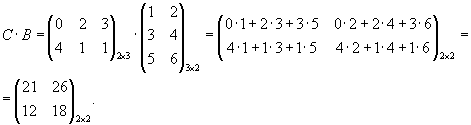
В · С¹С · В. Произведение матриц не коммутативно!

Пример 3. , ,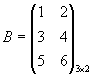

.

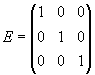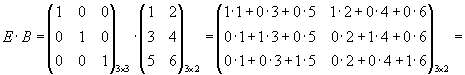
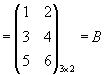А · Е=Е · А=А.

Приведем свойства операций над матрицами.

1. А · В В · А - произведение матриц не комму-

тативно.

2. А+В = В+А - сложение матриц коммутативно.

3. (А + В) +С = А + (В + С) - ассоциативность.

4. ,

5. ,

6. ,

7. - дистрибутивность.

8. - дистрибутивность.

9. А · Е=Е · А=А.

10. .

11. .

12. .