Достаточные признаки сходимости

числовых рядов с положительными членами

Теорема 1 (признак сравнения). Если члены двух числовых рядов и удовлетворяют неравенству для любых n, то из сходимости второго ряда следует сходимость первого ряда. Из расходимости первого ряда следует расходимость второго ряда.

Пример. Рассмотрим ряд . Сравним его с гармоническим рядом .

, .

По признаку сравнения данный ряд расходится.

Теорема 2 (признак Даламбера). Если для числового ряда существует конечный предел отношения последующего члена ряда к предыдущему

, то:

а) при ряд сходится;

б) при ряд расходится;

в) при вопрос о сходимости открыт.

Пример 1. , .

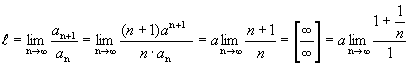= а,

при ряд сходится, ряд расходится.

Пример 2. .

=.

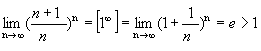Ряд расходится.