Линейные неоднородные
дифференциальные уравнения второго порядка
Пусть дано дифференциальное
уравнение
![]() (1)
(1)
и соответствующее ему однородное уравнение![]()
![]() . (2)
. (2)
Теорема 1. Общее решение неоднородного уравнения (1) можно
представить в виде суммы общего решения однородного уравнения (2) и любого частного решения неоднородного уравнения (1).
Доказательство.
Пусть ![]()
![]() - общее решение
однородного уравнения (2). Так как это уравнение второго порядка, то это
решение зависит от двух произвольных постоянных. Пусть
- общее решение
однородного уравнения (2). Так как это уравнение второго порядка, то это
решение зависит от двух произвольных постоянных. Пусть ![]() - какое-либо частное
решение неоднородного уравнения (1). Покажем, что их сумма
- какое-либо частное
решение неоднородного уравнения (1). Покажем, что их сумма ![]() является общим
решением неоднородного уравнения (1).
является общим
решением неоднородного уравнения (1).
Функция y зависит от
двух произвольных констант. Подставим y в (1).
![]() ,
,
![]() ,
,
0 +![]() .
.
Таким образом, у
является решением неоднородного уравнения (1) и так как оно зависит от двух
произвольных постоянных, то у является общим решением неоднородного
уравнения (1).
Для того чтобы найти общее решение неоднородного уравнения, надо найти
общее решение соответствующего однородного и какое-либо частное решение
неоднородного уравнения.
Для уравнения с постоянными коэффициентами частное решение
неоднородного уравнения подбирается по виду правой части f(x):
1) если f(x) - многочлен, то частное решение ищут в виде многочлена той же
степени с неизвестными коэффициентами;
2) если f(x) зависит от синуса и косинуса одного аргумента, то частное
решение ищут в виде суммы синуса и косинуса этого же аргумента с неизвестными
коэффициентами;
3) если в правой части -
показательная функция, умноженная на многочлен, то частное решение ищут в виде
произведения многочлена той же степени с неизвестными коэффициентами,
умноженного на показательную функцию с тем же аргументом, что и в уравнении.
Пример. ![]() - неоднородное уравнение.
- неоднородное уравнение.
![]() - соответствующее ему однородное
уравнение.
- соответствующее ему однородное
уравнение.
![]() ,
, ![]() ,
, ![]() .
.
![]() - общее решение однородного
уравнения.
- общее решение однородного
уравнения.
Будем
искать частное решение неоднородного уравнения в виде
![]() .
.
Подставим эту функцию в неоднородное уравнение:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Приравняем
коэффициенты при sinx и cosx.
![]()
![]()
![]()
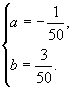
![]() - частное решение неоднородного
уравнения.
- частное решение неоднородного
уравнения.
![]() - общее решение неоднородного
уравнения.
- общее решение неоднородного
уравнения.