Интегрирование тригонометрических выражений

1. Интегралы от произведений синуса и косинуса разных аргументов.

ò sin mx cos nx dx,

ò sin mx sin nx dx,

ò cos mx cos nx dx.

Данные интегралы сводятся к табличным с помощью формул преобразования произведения в сумму:

sin a cos b=1/2(sin(a-b)+sin(a+b)),

sin a sin b=1/2(cos(a-b)-cos(a+b)),

cos a cos b=1/2(cos(a-b)+cos(a+b)).

Пример.

=

2. Интегралы от степеней синуса и косинуса одного аргумента.

ò sin^m x cosⁿ x dx.

1) Если хотя бы одно из чисел m и n нечетно, то от нечетной степени отделяют один сомножитель и вносят его под знак дифференциала. Подынтегральную функцию приводят к одной из тригонометрических функций.

Пример. ò sin⁵x cos⁴x dx = ò sin⁴x cos⁴x sin x dx =

= -ò (1-cos²x)²cos⁴x d(cosx) = -òcos⁴x d(cosx) + 2ò cos⁶x d(cosx) -

- òcos⁸x d(cosx) = .

2) Обе степени четные. В этом случае применяют формулы понижения степени

, , ,

до тех пор, пока не появятся нечетные степени тригонометрических функций.

3. Интегралы от рациональной функции, содержащей синус и косинус.

Рассмотрим интеграл вида

.

Этот интеграл рационализируется универсальной подстановкой

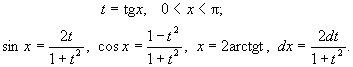
Пример.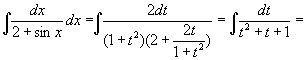

=