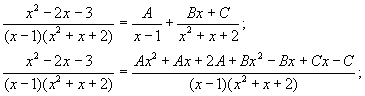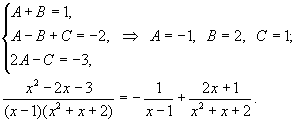Интегрирование рациональных функций

Определение. Функция называется рациональной, если ее можно представить в виде дроби

,

где P(x) и Q(x) – многочлены.

Из класса всех дробей выделяют основные простые дроби:

где a, p , q, M, N ÎR , kÎ N.

Интегралы от первых двух типов простых дробей находятся с помощью подстановки t = x-a:

,

=.

Интеграл от третьего типа простых дробей рассмотрим в предположении, что знаменатель не имеет корней, т.е. q - p² >0. Выделим полный квадрат в знаменателе

,

где a² = q - p² >0.

=

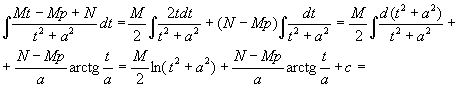
Если степень числителя выше степени знаменателя, то дробь называется неправильной; в таком случае выполнив деление, получим

,

где W(х) - некоторый многочлен, а второе слагаемое представляет собой правильную дробь, у которой степень числителя меньше степени знаменателя. Например, рассмотрим неправильную дробь

.

Разделим числитель на знаменатель

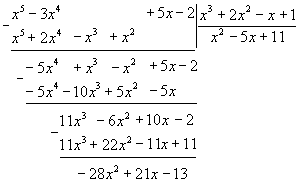
и выделим целую часть дроби

.

Целая часть дроби легко интегрируется. Следовательно, вопрос об интегрировании рациональной функции сводится к вопросу об интегрировании правильных дробей. Любую правильную дробь можно представить в виде суммы простых дробей с помощью следующих теорем.

Теорема 1. Каждый многочлен Q(x) с действительными коэффициентами может быть представлен единственным образом в виде

, (1)

где a, b, …,- корни многочлена кратности k, l, … ; квадратичные множители кратности m, n,… не имеют действительных корней.

Теорема 2. Пусть R(x)/Q(x) - правильная рациональная дробь, у которой знаменатель представлен в виде (1). Тогда эту дробь можно единственным образом представить в виде суммы простых дробей:

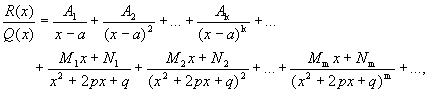, (2)

где - некоторые действительные числа.

Выражение (2) называется разложением рациональной дроби на простые дроби, числа - коэффициентами разложения.

Следствие. Пусть R(x)/Q(x) - правильная рациональная дробь, у которой знаменатель - многочлен степени n, имеющий n различных действительных корней . Тогда эту дробь можно единственным образом представить в виде суммы простых дробей:

, (3)

где - некоторые действительные числа.

Для определения коэффициентов разложения используют метод неопределенных коэффициентов, который состоит в следующем: приводят левую часть равенства (2) или (3) к общему знаменателю и приравнивают коэффициенты при одинаковых степенях многочлена, полученного в числителе и многочлена R(x).

Пример 1. Разложим дробь на простые дроби. Знаменатель имеет два корня - 1 и 2. Воспользуемся формулой (3).

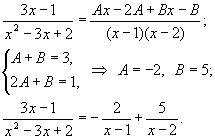
Пример 2. Разложим дробь на простые дроби. Квадратичный множитель в знаменателе не имеет корней. Воспользуемся формулой (2).