Приложения определенного интеграла

Вычисление площадей фигур, расположенных под (над) графиком функции на некотором отрезке

Это приложение вытекает из геометрического смысла определенного интеграла (рис. 1).

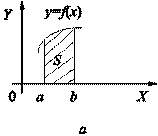
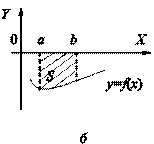
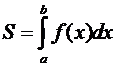
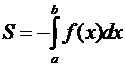
Рис. 1

Вычисление площади фигур, ограниченных графиками двух функций на некотором отрезке

S = S₂ – S₁ = = ,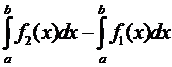

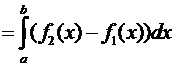где S₁ и S₂ — площади криволинейных трапеций под графиками функций y = f₁(x) и y = f₂(x) (рис. 2).

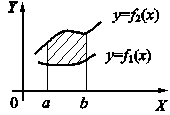
Рис. 2

Пример 1. Найти площадь фигуры, ограниченной линиями y = x² – 1, y = x + 1 (рис. 3).

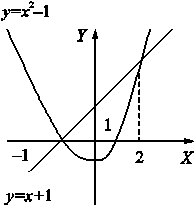
Рис. 3

Найдем абсциссы точек пересечения.

x² –1 = x + 1,

x² – x – 2 = 0,

x₁ = 2 x₂ = –1.

.

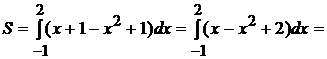
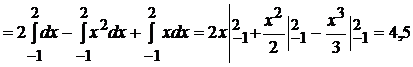Вычисление объемов тел, полученных от вращения графика функции вокруг оси ОХ

Объем тела, полученного от вращения графика функции вокруг оси ОХ на отрезке [a, b] (рис. 4)

Рис. 4

вычисляется по формуле:

.

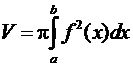Пример 2. Найти объем тела, полученного от вращения графика функции y = sinx вокруг оси ОХ на отрезке x Î [0,p] (рис. 5).

Рис 5

.
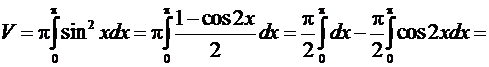
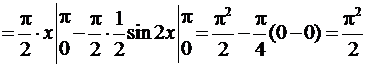