Применение понятия производной в экономике

Предельная себестоимость

Рассмотрим зависимость C = f(Q) себестоимости С  произведенной продукции от ее объема Q. Предельная себестоимость характеризует отношение прироста себестоимости DC к приросту объема продукции DQ при малом изменении объема продукции.

.

Эластичность спроса

Пусть D=D(P) – функция спроса от цены товара Р. Под эластичностью спроса понимается относительное изменение спроса при изменении цены товара на 1 %:

.

При непрерывной зависимости DD от DP удобно перейти к пределу при DP®0:

(4.1)
 
.

Эластичность спроса можно представить в следующем виде:

.

Из этого равенства следует, что эластичность спроса обладает свойствами логарифма:

.

Так как D(P) - убывающая функция, то . Из формулы (4.1) следует, что E(D)<0.

Различают три вида спроса в зависимости от величины ½E(D)½:

1)  ½E(D)½>1  (E(D)< -1) – спрос эластичен;

2)  ½E(D)½=1  (E(D)= -1) ) – спрос нейтрален;

3)  ½E(D)½<1  (E(D)> -1) ) – спрос неэластичен.

Найдем изменение выручки с увеличением цены товара при разных вариантах эластичности спроса. Выручка  I  равна произведению цены товара P на величину спроса D:

I(P)=D(P) P.

Найдем производную этой функции:

.

Выразим  из формулы (4) и подставим в последнее равенство:

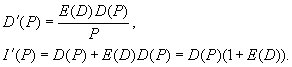
Возможны случаи:

1)  если  E(D)< -1, то  <0  -  при эластичном спросе повышение цены товара ведет к снижению выручки;

2)  если  E(D)= -1, то  =0  -  при нейтральном спросе изменение цены не влияет на выручку;

3)  если  E(D)> -1, то  >0  -  при неэластичном спросе повышение цены товара приводит к росту выручки.

Максимизация прибыли

Пусть Q – количество реализованного товара, R(Q) – функция дохода, C(Q) – функция затрат на производство товара. Тогда прибыль от реализации товара выражается формулой

П(Q) = R(Q) – C(Q).

Чтобы прибыль была максимальной при некотором значении Q, должен выполняться необходимый принцип экстремума . Следовательно,

,

где   - предельный доход:

  - предельные издержки.

Получено известное микроэкономическое утверждение: для того чтобы прибыль была максимальной, необходимо, чтобы предельный доход и предельные издержки были равны.

Закон убывающей эффективности производства

Рассмотрим функцию, выражающую зависимость объема произведенной продукции V от капитальных затрат К. Характерный вид этой функции дается уравнением

,

где a, b, c –известные положительные числа, определяемые структурой производства, Vlim – предельно возможный объем выпускаемой продукции.

Найдем вторую производную данной функции.

           

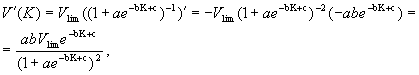
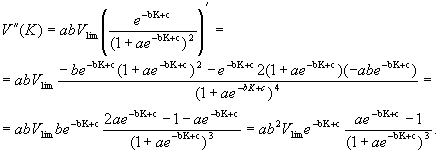
Определим критическую точку второй производной из условия .

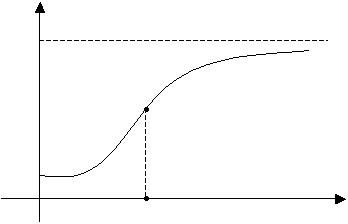
Точка Ккр  является точкой перегиба графика функции:

1)     при К< Ккр  >0  - график вогнутый, увеличение капитальных затрат приводит к интенсивному росту выпуска продукции.

2)     при К> Ккр  <0  - график выпуклый, прирост объема выпуска продукции снижается, эффективность увеличения капитальных затрат падает.

График данной функции имеет следующий вид:

                                                                                                                                

                             V                                                                                      

                                                                                                                                

                         Vlim                                                                                      

                                                                                                                                

                                                                                                                                

                                                                                                                                 

                                                                                                                                

                                                                                                                                

                                                                                                                                

                                                                                                                                

                             0                            Kкр                                          K        

                                                                                                                                

В стратегии капиталовложений важно определить критический объем затрат, сверх которого дополнительные затраты будут приводить ко все меньшей отдаче при имеющейся структуре организации производства.