Сравнение бесконечно малых функций

Пусть б.м. функции при . Предположим, что существует предел их отношения и он равен l.

.

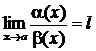Тогда если:

1) l=1, то функции и называются эквивалентными б.м.;

2) l - число, l¹0, то функции и называются б.м. одинакового порядка;

3) l=0, то функция называется б.м. более высокого порядка, чем ;

4) l= ±¥, то функция называется б.м. более высокого порядка, чем .

Пример 1. , ,

,

и - эквивалентные б.м. функции.

Пример 2. =х³,

=х,

,

,

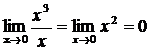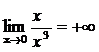- б.м. функция более высокого порядка, чем .