Понятие функции
Пусть Х и Y - некоторые множества.
Определение 1. Если каждому элементу xÎХ ставится в соответствие по некоторому правилу единственный элемент yÎ Y , то говорят, что на множестве Х задана функция (отображение) со значениями в множестве Y :
f : X®Y,
y=f(x).
Множество Х называется областью определения функции и обозначается Dom(f) или D(f), множество Y называется множеством значений функции и обозначается Im(f) или I(f).
Определение 2. Если функция f переводит
элемент xÎХ в элемент yÎ Y,
т.е. y=f(x), то у называют образом
элемента х, а х называют прообразом элемента у. Образ
всегда единственен.
Определение 3. Композицией отображений f : X®Y и g : Т®Х называется отображение f · g : Т®Y.
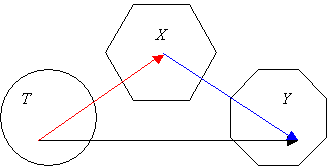
g f
g
· f
Если f и g – числовые функции, то их композицию называют сложной функцией:
y=f(x), u=g(t)
Þ
y=f(g(t)).
Пример. y=x3, x=sint Þ
y=sin3t.
Определение 4. Если обратное соответствие, переводящее У в Х является функцией, т.е. у каждого элемента yÎУ имеется единственный прообраз xÎХ, то это соответствие называют обратным отображением, или обратной функцией.
f -1 : Y®Х, х=f -1 (у).
Обратная функция обратима, и обратная функция к обратной функции совпадает с исходной функцией (f -1) -1= f .
Пример. Рассмотрим функцию y=х2. Выразим х: ![]() . Обратной функцией будет являться
. Обратной функцией будет являться ![]() .
.
Определение 5. Графиком числовой функции y=f(x) называется совокупность точек плоскости вида (x , f(x)), где хÎD(f).
Графики взаимно обратных функций симметричны относительно биссектрисы I и III координатных углов.
Определение 6. Числовая функция y=f(x) называется монотонно возрастающей (убывающей), если большему значению аргумента соответствует большее (меньшее) значение функции:
"x1, x2ÎD(f) : x1>x2 Þf(x1)>f(x2) (или f(x1)<f(x2) ).
Определение 7. Числовая функция y=f(x) называется ограниченной сверху на множестве АÌ D(f), если найдется число М такое, что
"xÎА f(x)<М.
Определение 8. Числовая функция y=f(x) называется ограниченной снизу на множестве АÌ D(f), если найдется число m такое, что
"xÎА f(x) >m.
Определение 9. Числовая функция y=f(x) называется ограниченной на множестве АÌ D(f), если найдется число K такое, что:
"xÎА ïf(x)ï<K.
Пример 1. Функция y=sinx ограничена, так как ïf(x)ï<2 "xÎ R.
Пример 2. Функция y=2-x2 ограничена сверху, так
как f(x)<3 "xÎ R.
Определение 10. Если числовая функция y=f(x) принимает одно и то же значение с на множестве АÌ D(f), то говорят, что функция тождественно равна с на множестве А, и обозначают f(x) º с.