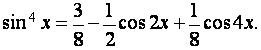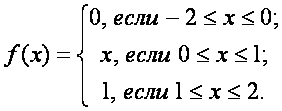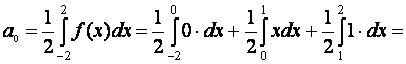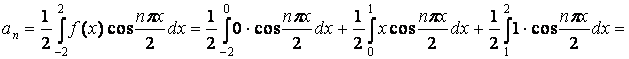Примеры разложения некоторых функций в ряд Фурье

Пример 1. Разложим в ряд Фурье функцию при и найдем с помощью полученного разложения суммы числовых рядов:

а) ;

б) ;

в) .

Т.к. функция четная, то ее разложение в ряд Фурье будет содержать только косинусы, поэтому следует вычислить только

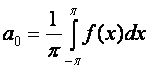и ,

а затем составить ряд:

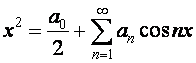при .

.

==

=

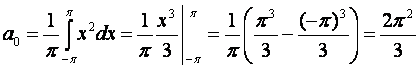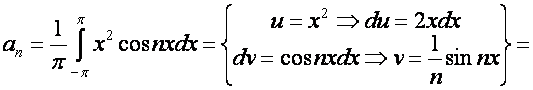
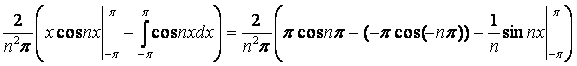Итак,

.

а) При получаем

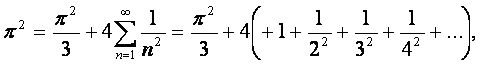
Откуда

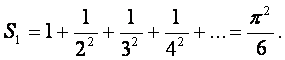
б) При получаем

откуда

в) Заметим, что , откуда

.

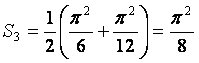Ответ:

;

а) 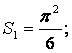б) в)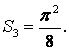

Пример 2. Теперь разложим в ряд Фурье ту же функцию , но при

.

Разложение четной функции надо произвести по несимметричному промежутку, поэтому в отличие от предыдущего примера оно будет полным:

.

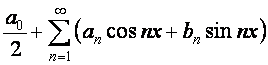При этом коэффициенты Фурье вычисляются интегрированием по отрезку , но т.к. значения функции в концах отрезка не совпадают, то сумма ряда Фурье равна исходной функции лишь в интервале .

.

.

.

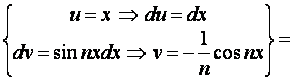
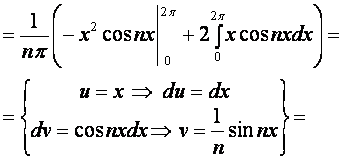
Итак,

для .

Ответ:

Пример 3. Разложим в ряд Фурье функцию

В данной задаче l =2, причем для вычисления коэффициентов Фурье промежуток интегрирования согласно заданной функции следует разбить на две части: (-2;0) и (0;2) и в каждом из отрезков функция имеет разный вид. Так

=

=

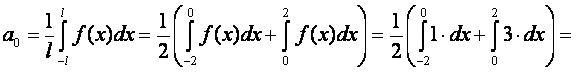
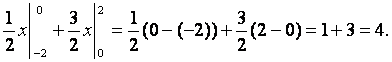
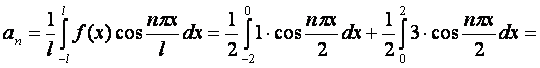
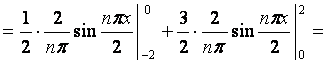
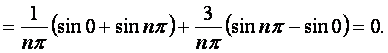
значит,

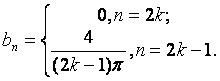
Следовательно,

.

Ответ:

для

Пример 4. Разложим в ряд Фурье тригонометрический многочлен

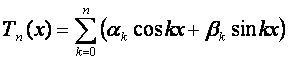
на промежутке длиной .

Так как все слагаемые представляют собой линейные комбинации тригонометрической системы функций:

1, …, …, ортогональной на промежутке длины , то сам многочлен представляет собой свое разложение в требуемый ряд Фурье.

Пример 5. Разложим в ряд Фурье функцию на промежутке длиной .

Число для заданной функции является одним из периодов, но она не входит в тригонометрическую систему, приведенную в примере 8. Выразим заданную функцию через функции 1, и , т.е. понизим показатель степени синуса до первой:

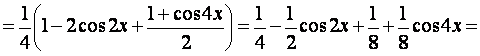
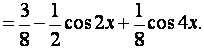
Это и будет ряд Фурье заданной функции.

Ответ:

Пример 6. Разложим в ряд Фурье функцию

В задаче , т.е. l = 2, причем для вычисления коэффициентов Фурье промежуток интегрирования согласно заданной функции следует разбить на три части: [-2; 0] ; [0; 1] и [1; 2]. При этом в каждом из отрезков функция имеет разный вид:

=

;

=

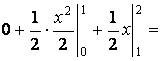
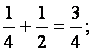
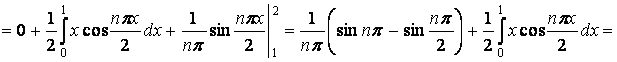
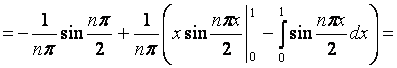
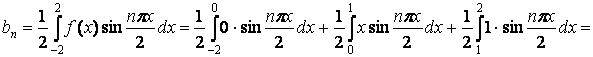
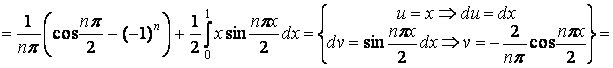
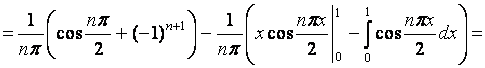
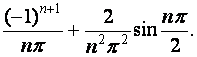
Следовательно,

.

Ответ:

при