Ряд
Фурье непериодической функции
Пусть функция f(x) задана
на отрезке 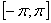 и является на нем кусочно дифференцируемой. На этом же отрезке построим
функцию
и является на нем кусочно дифференцируемой. На этом же отрезке построим
функцию
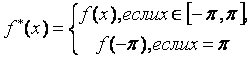
И продолжим ее периодически (с периодом Т=2π) на всю числовую прямую.
Введенная функция 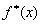 сохраняет кусочную
дифференцируемость функции f(x) на отрезке
сохраняет кусочную
дифференцируемость функции f(x) на отрезке 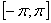 и отличается на нем от
f(x) разве лишь в одной точке. Поэтому при вычислении коэффициентов Фурье для
функции
и отличается на нем от
f(x) разве лишь в одной точке. Поэтому при вычислении коэффициентов Фурье для
функции 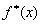 по формулам (3) мы
фактически получаем коэффициенты Фурье функции сс т.к. изменение значений
функции в конечном числе точек не меняет величины интеграла.
по формулам (3) мы
фактически получаем коэффициенты Фурье функции сс т.к. изменение значений
функции в конечном числе точек не меняет величины интеграла.
Для любой внутренней точки хо из
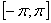 будет справедлива
формула
будет справедлива
формула
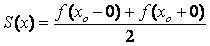 .
.
.
Для точек 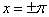 при упрощающим
ситуацию предположении непрерывности f(x) в этих точках получаем:
при упрощающим
ситуацию предположении непрерывности f(x) в этих точках получаем:
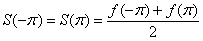 т.к.
т.к. 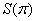 непериодическая и
непериодическая и 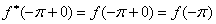 , а
, а 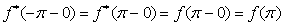 .
.
Пример 1. Разложим функцию 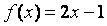 в ряд Фурье на
в ряд Фурье на 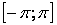 .
.
Решение:
Очевидно, f(x) дифференцируема на 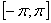 . Найдем коэффициенты Фурье :
. Найдем коэффициенты Фурье : 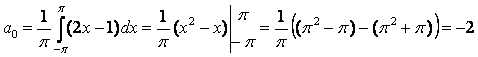 ;
;
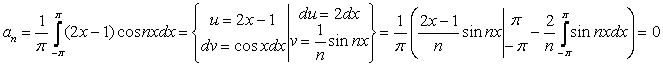
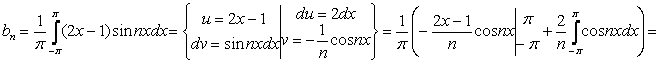
 .
.
Итак, ряд Фурье имеет вид 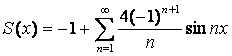 .
.
Т.к.
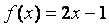 непрерывна
на
непрерывна
на 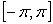 , то
, то 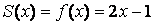 при
при 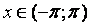 , а
, а 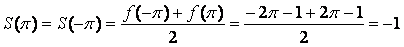 , значит,
, значит,
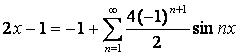 при
при 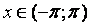 .
.
Пример 2. Разложим функцию 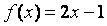 и ряд Фурье на
и ряд Фурье на 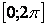 .
.
Решение: Если бы f(x) была 2π—периодической,
ее ряд Фурье на 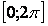 имел бы точно такой же
вид, что и на
имел бы точно такой же
вид, что и на 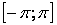 , но
, но 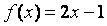 на
на 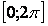
не
является 2π—периодической
функцией. Однако 2π—периодичность
тригонометрической системы функций позволяет найти коэффициенты Фурье по
формулам, аналогичным формулам
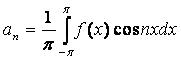 ,
, 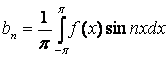 ,
,
с
заменой отрезка интегрирования на любой другой отрезок длиной 2π:

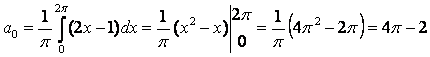 ;
;
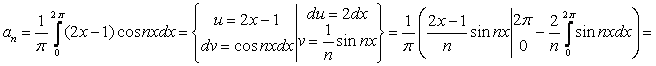
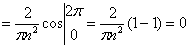 ;
;
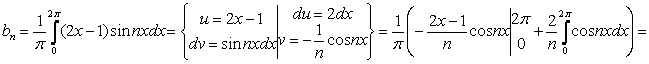
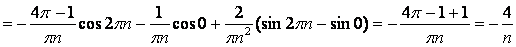 .
.
Итак, ряд Фурье имеет вид 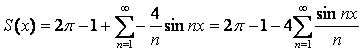 ,
,
а 
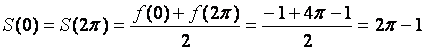 ,
,
значит, 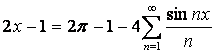 ,
, 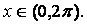
Если необходимо разложить в ряд Фурье кусочно
дифференцируемую функцию f(x) заданную лишь на отрезке 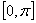 , то ее можно продолжить произвольным образом в
, то ее можно продолжить произвольным образом в 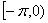 с сохранением кусочной дифференцируемости и получить при этом бесконечное
множество различных разложений (
совпадающих численно лишь в (о, π)). Вызывают
интерес два «специальных продолжения: четное и нечетное».
с сохранением кусочной дифференцируемости и получить при этом бесконечное
множество различных разложений (
совпадающих численно лишь в (о, π)). Вызывают
интерес два «специальных продолжения: четное и нечетное».
1). Если новая функция 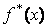 четная, то по
свойствам интеграла от четной и нечетной функции по симметрическому промежутку
четная, то по
свойствам интеграла от четной и нечетной функции по симметрическому промежутку
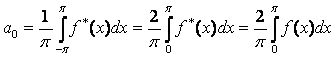 ,
,
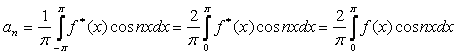 ,
,
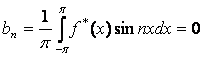 ,
,
т.е. коэффициенты Фурье
вычисляются по формулам:
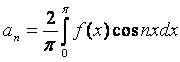 ,
, 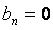 , здесь
, здесь 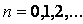 (1)
(1)
В результате
использовании формул (1) получаем так называемое разложение по косинусам: 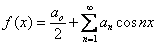 .
.
2). Если новая функция 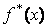 нечетная, то
нечетная, то
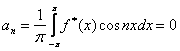 , здесь
, здесь 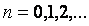
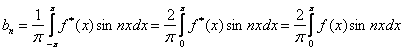 ,
, 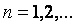 , т.е. коэффициенты Фурье вычисляются по формулам:
, т.е. коэффициенты Фурье вычисляются по формулам:
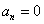 , здесь
, здесь 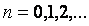 ;
; 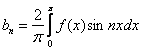 ,
, 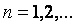 (2)
(2)
В результате использовании формул (2) получаем так называемое
разложение по синусам: 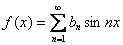 .
.
При этом даже в случае непрерывности f(x) на 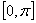 оба разложения ведут
себя по-разному: при разложении по косинусам
оба разложения ведут
себя по-разному: при разложении по косинусам
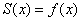 на
на
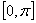 ; при разложении по синусам
; при разложении по синусам
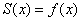 на (0,π), а
на (0,π), а 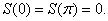
Пример 3.
Разложим функцию 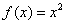 по косинусам на
отрезке
по косинусам на
отрезке 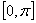 .
.
Решение: 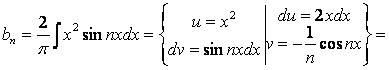
=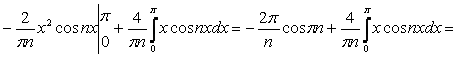
=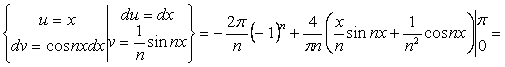
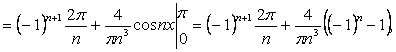
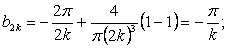
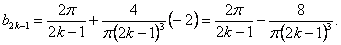
Итак, 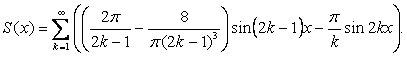
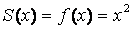 при
при 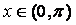 ,
, 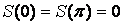 .
.
Ответ:
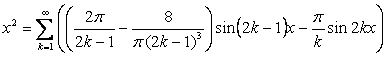 ,
, 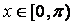 .
.
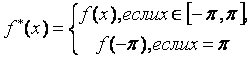
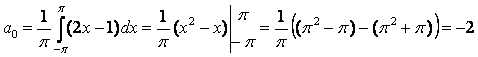 ;
;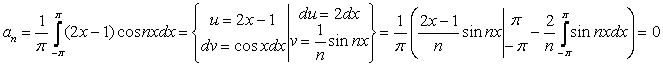
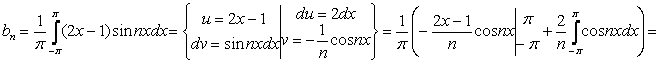
 .
.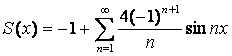 .
.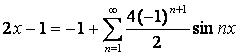 при
при 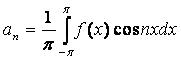 ,
, 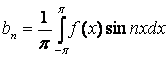 ,
,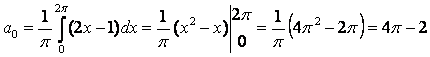 ;
;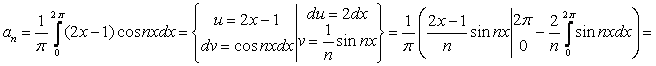
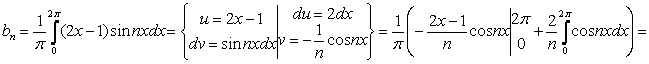
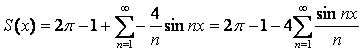 ,
,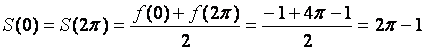 ,
, 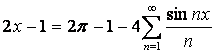 ,
, 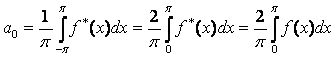 ,
,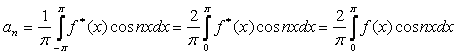 ,
,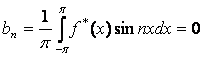 ,
,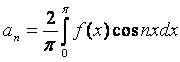 ,
, 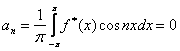 , здесь
, здесь 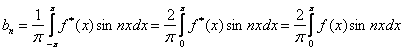 ,
, 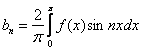 ,
, 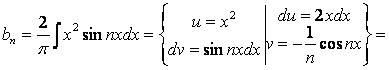
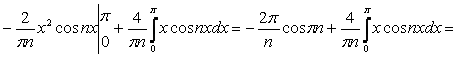
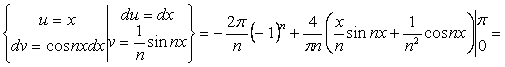
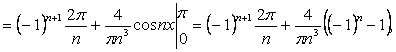
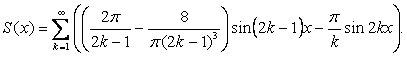
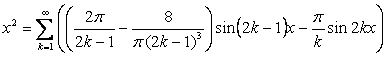 ,
,