Понятие ортогональной
системы функций
Определение1. Система (множество, совокупность)
функций, определенных на отрезке ![]() , называется ортогональной
на этом отрезке, если
, называется ортогональной
на этом отрезке, если 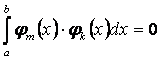 при
при ![]() и
и
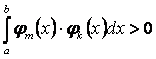 при
при ![]() , то есть
, то есть 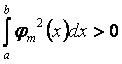 .
.
Определение 2. Система
функций 1, cosx,
sinx, cos2x,
sin2x,…,cosnx, sinnx
называется тригонометрической.
Заметим, что все функции, входящие в
систему:
φ1(х)=1,![]() φ2(х)=cosx,
φ2(х)=cosx,![]() φ3(х)=sinx,
φ3(х)=sinx,![]() φ4(х)=cos2x,
φ4(х)=cos2x,![]() φ5(х)=sin2x,…
φ5(х)=sin2x,…
являются периодическими с общим наименьшим положительным
периодом 2π.
В самом деле, φ1(х)=1—периодическая
с любым, отличным от нуля периодом,
функции φ2(х)=cosx и φ3(х)=sinx имеют наименьший положительный
период 2π, а функции cosпx и![]() sinпx имеют
наименьший положительный период
sinпx имеют
наименьший положительный период ![]() . Поэтому число Т = 2π
является с одной стороны общим, а с другой стороны наименьшим положительным периодом для всех функций,
входящих в систему.
. Поэтому число Т = 2π
является с одной стороны общим, а с другой стороны наименьшим положительным периодом для всех функций,
входящих в систему.
Теорема 1. Интеграл
от периодической функции по любому отрезку, длина которого равна положительному
периоду, не зависит от выбора отрезка интегрирования.
Действительно, пусть Т > 0 - период функции f(x),
а – произвольное
действительное число. Докажем, что
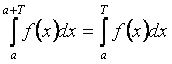 .
.
По свойству аддитивности определенного интеграла
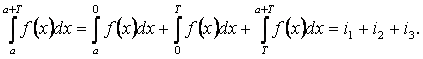
В интеграле i3 сделаем замену переменной: пусть x=t+T, тогда t=x-T, dx=dt, tв =a+T-T= a; t н = T-T = 0:
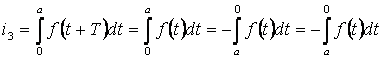
(т.к. определенный интеграл
не зависит от обозначения переменной интегрирования).
Получили: i3=-i1, следовательно  , что и требовалось доказать.
, что и требовалось доказать.
Теорема 2. Тригонометрическая система функций ортогональна на любом отрезке длины
2π.
Учитывая утверждение теоремы 1, доказательство проведем для симметричного
отрезка ![]() .
.
Сначала докажем ортогональность функции φ1(х)=1
ко всем остальным:
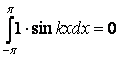 ,так как при любом натуральном k функция
,так как при любом натуральном k функция ![]() нечетная, а отрезок
интегрирования симметричен.
нечетная, а отрезок
интегрирования симметричен.
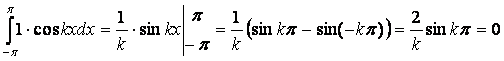 .
.
Теперь докажем ортогональность
всех синусов всем косинусам:
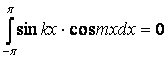 при любых k и m
при любых k и m ![]() N (даже при любом k = m), т.к. подынтегральная функция
нечетная.
N (даже при любом k = m), т.к. подынтегральная функция
нечетная.
Далее докажем ортогональность косинусов с разными
аргументами, т.е. при k ≠ m: 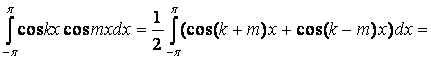
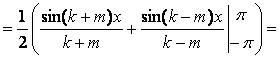
![]() ,
,
т.к. ![]() при любом р.
при любом р.
Теперь проверим ортогональность синусов с различными аргументами, т.е.
при k≠m:
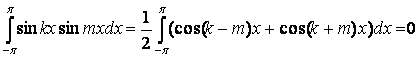
(см. предыдущий интеграл).
Осталось вычислить интегралы от квадратов функций системы:
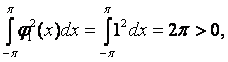
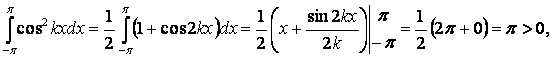
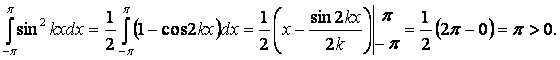
Теорема доказана.
Определение 3. Функциональный ряд
вида
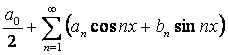 , (1)
, (1)
составленный из функций
тригонометрической системы с
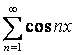 .
.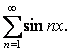
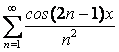 .
.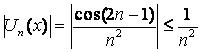 .
.