Применение функций

нескольких переменных в экономике

 

Прибыль от производства товаров разных видов

Пусть х1, х2, …, хm - количество производимых т разновидностей товара, а их цены, соответственно, - Р1, Р2, …, Рm (все Рi - постоянные величины). Пусть затраты на производство этих товаров задаются функцией издержек

.

Тогда функция прибыли имеет вид

.

Максимум прибыли будем искать как условие локального экстремума функции многих переменных при ³ 0:

Это условие приводит к системе алгебраических уравнений относительно переменных хi

Система уравнений реализует известное правило экономики: предельная стоимость (цена) товара равна предельным издержкам на производство этого товара. Решениями этой системы уравнений являются т-мерные точки.

Пример. Пусть производится два вида товаров, обозначим их количества через х и у. Пусть цены на эти товары, соответственно, Р1=8 и Р2 = 10, а функция затрат С= х2 + ху + у2. Найти максимум прибыли. Прибыль выражается функцией

.

Условия локального экстремума приводят к системе линейных алгебраических уравнений

решение которой определяет точку (2, 4). Поскольку

D=AC-B =3>0, A=-2<0,

то найденная точка определяет локальный максимум функции прибыли, который равен Пmax = 28.

 

Оптимальное распределение ресурсов

Рассмотрим задачу оптимального распределения ресурсов на примере функции выпуска  при допущении, что функция затрат на ресурсы х и у линейна, т.е. имеет вид , где Р1  и Р2 - соответствующие цены на эти факторы.

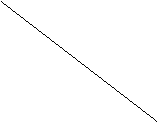
В точке (x0, y0) оптимального распределения ресурсов линии уровня функций выпуска и затрат касаются.

 

                                                                                                                                

                                                Y                                                                              

                                                                                                               

                                               A/P                                                                            

                                                                                                                                

                                                                                                                                

                                                y0                                                                             

                                                                                                                                

                                                                                                                                

                                                                                                                                

                                                                                                                                

                                                    0                 x0                    A/P       X                   

Эти линии определяются, соответственно, уравнениями:

 или ,

где С>0 и А>0 - постоянные числа, b=С/а0. Условие касания этих линий определяется уравнением

.

.

Из этого уравнения находится значение . Тогда из уравнения линии уровня функции выпуска определяется значение . Отсюда получаем, что оптимальное распределение ресурсов  должно быть произведено в отношении .

 

Оптимизация спроса

Задачей исследования спроса является оптимизация функции полезности при ограничениях на бюджет покупателя. Рассмотрим пример: найти величины спроса х и у на две разновидности товара при ценах на них, соответственно, a и b, если потребитель при бюджете К стремится максимизировать функцию полезности, которая имеет вид

.

(12)
 
Из условия задачи следует, что на покупку, стоимость которой ax + by, потребитель может израсходовать сумму, не превышающую К. Следовательно, необходимо найти точку (х, у), в которой функция полезности достигает максимума при ограничениях:

.

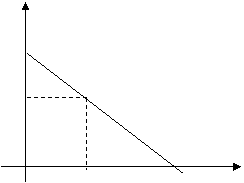
Ограничения (12) задают на плоскости Оху замкнутую область D в виде треугольника, в которой следует искать точку максимума функции F(x,y).

                                                Y                                                                              

                                                                                                                                 

                                               K/b                                                                            

                                                                                                                                

                                                                        (K/(a+b);K/(a+b))                           

                                                                                                                                

                                               F=0                                                                          

                                                                                                                                

                                                                                                                                

                                                    0                 F=0                  K/a       X                

Вычислив частные производные функции полезности, находим, что единственная критическая точка (0, 0) находится на границе области D; и в ней, как и на граничных линиях х = 0 и у = 0, функция F(x, у) = 0, что является минимальным ее значением. Следовательно, нужно искать точку максимума этой функции на границе

ax + by = К

области D. Подставляя из этого уравнения выражение для у в функцию F(x, у), получаем функцию одной переменной

.

Критическую точку этой функции найдем из условия обращения в нуль ее первой производной; получаем, что х=К/(а+b), откуда у=К/(а+b). Таким образом, в данной модели оптимальный спрос на оба вида товаров одинаков: он пропорционален бюджету и обратно пропорционален суммарной цене товара.