Построение эмпирических формул

методом наименьших квадратов

 

Имеются две переменные х и y и таблица эмпирических значений этих переменных.

x

x1

x2

…

xn

y

y1

y2

...

yn

 

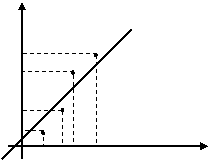                             Y

 

                            y4

                            y3

 

                            y2

                            y1

 

                              0     x1 x2 x3  x4                           X

 

 

Известно, что зависимость между переменными y и x близка к линейной. Требуется найти теоретическую функциональную зависимость между y и x. Будем искать эту зависимость в виде линейной функции .

Подставляя значения переменной х из таблицы в уравнение , найдем теоретические значения переменной у. Составим разности между теоретическими и эмпирическими значениями переменной у.

            

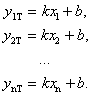
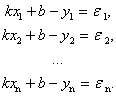
Величины e1, …, en называются погрешностями. Подберем параметры прямой так, чтобы она проходила как можно ближе ко всем точкам одновременно. Для этого найдем сумму квадратов погрешностей  и выберем k и b так, чтобы эта сумма была минимальной. Выразим суммарную погрешность:

.

Рассмотрим функцию .

Найдем частные производные этой функции и приравняем их к нулю.

.

Получена система из двух линейных уравнений с двумя неизвестными k и b. Данная система называется нормальной системой метода наименьших квадратов.

Уравнение  называется уравнением линейной регрессии.

Пример. В таблице приведены эмпирические значения двух переменных Х и У. В этой же таблице рассчитаем значения величин ХY и X2. В последнем столбце найдем суммы этих величин.

                                                                                                                                             S

Y

1

3

2

4

10

X

-2

1

3

4

6

Х2

4

1

9

16

30

ХY

-2

3

6

16

23

 

- нормальная система метода наименьших квадратов.

Решим ее.

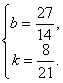
                     - уравнение линейной регрессии.

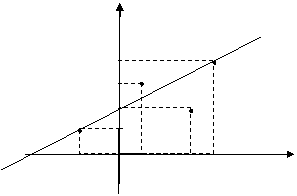
Построим на одном чертеже эмпирические точки и теоретическую линию.

 

 

 

                                      Y

 

 

                                      4

                                      3

                                  

                                      2

                                           1

 

                 -4,5     -2     0     1          3    4                  X