Допустимые решения системы

линейных уравнений и неравенств

Пусть дана система из m линейных уравнений и неравенств с n неизвестными.

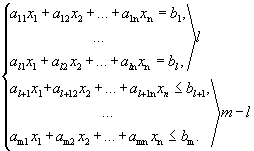
Определение 1. Точка Rⁿ называется возможным решением системы, если ее координаты удовлетворяют уравнениям и неравенствам системы. Совокупность всех возможных решений называется областью возможных решений (ОВР) системы.

Определение 2. Возможное решение, координаты которого неотрицательны, называется допустимым решением системы. Множество всех допустимых решений называется областью допустимых решений (ОДР) системы.

Теорема 1. ОДР является замкнутым, выпуклым, ограниченным (или неограниченным) подмножеством в Rⁿ.

Теорема 2. Допустимое решение системы является опорным тогда и только тогда, когда эта точка является угловой точкой ОДР.

Теорема 3 (теорема о представлении ОДР). Если ОДР - ограниченное множество, то любое допустимое решение можно представить в виде выпуклой линейной комбинации угловых точек ОДР (в виде выпуклой линейной комбинации опорных решений системы).

Теорема 4 (теорема о существовании опорного решения системы). Если система имеет хотя бы одно допустимое решение (ОДРÆ), то среди допустимых решений существует хотя бы одно опорное решение.