Решение систем линейных неравенств

Определение 1. Совокупность точек пространства Rⁿ, координаты которых удовлетворяют уравнению а₁х₁+ а₂х₂+…+a_nx_n = b, называется (n - 1)-мерной гиперплоскостью в n-мерном пространстве.

Пример. n=2 , - уравнение прямой на плоскости.

n=3 , - уравнение плоскости в пространстве.

Теорема 1. Гиперплоскость делит все пространство на два полупространства. Полупространство является выпуклым множеством.

Пересечение конечного числа полупространств является выпуклым множеством.

Теорема 2. Решением линейного неравенства с n неизвестными

а₁х₁+ а₂х₂+…+a_nx_n b

является одно из полупространств, на которые все пространство делит гиперплоскость

а₁х₁+ а₂х₂+…+a_nx_n = b.

Рассмотрим систему из m линейных неравенств с n неизвестными.

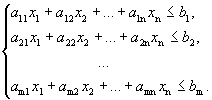
Решением каждого неравенства системы является некоторое полупространство. Решением системы будет являться пересечение всех полупространств. Это множество будет замкнутым и выпуклым.