Евклидово пространство. Выпуклые
множества
Определение
1. Упорядоченная совокупность из n действительных
чисел 
называется n-мерной точкой.
Определение
2. Расстоянием между двумя n-мерными точками 
и 
называется
величина
.
Определение
3. Совокупность
всех n-мерных
точек с введенной на ней метрикой 
называется n-мерным евклидовым
(метрическим) пространством Rn.
Определение
4. ε-окрестностью
точки 
в Rn называется
множество точек 
, удовлетворяющих условию 
.
Определение
5. Множество
А 
Rn называется открытым, если любая точка входит в него вместе с некоторой
окрестностью.
Определение 6. Множество B Rn называется замкнутым, если оно
является дополнением до некоторого открытого множества.
В — замкнутое ó Rn \ B —
открытое.
Определение 7. Отрезком в Rn, соединяющим точки 
и 
, называется множество точек, удовлетворяющее условию
.
Определение
8. Множество А Rn называется
выпуклым, если вместе с любыми двумя точками, входящими в него, оно содержит
отрезок, их соединяющий (рис. 1 а, б), остальные множества называются
невыпуклыми (рис. 1 в, г).
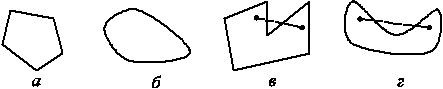
Рис. 1
Определение
9.
Точка х 
Rn называется
угловой точкой множества А (рис.
2), если она не является внутренней ни для какого отрезка, целиком
лежащего в А.
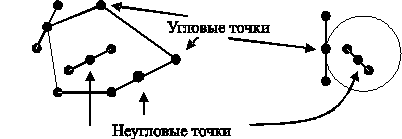
Рис. 2
Теорема
1. Пересечение
конечного числа выпуклых множеств есть выпуклое множество.
Доказательство.
Пусть А и В — выпуклые множества.
Докажем,
что 
— выпуклое множество.
Пусть
х, у
.
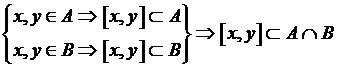Следовательно,
— выпуклое множество.