Дифференциальные уравнения

Задача 1. Найти общее решение дифференциального уравнения x у'-у = x ²е^x и частное решение, удовлетворяющее начальному условию у₀ =0 при х₀ =1.

Решение. Это линейное дифференциальное уравнение первого порядка. Оно приводится к виду . Для этого поделим обе части этого уравнения на х. Получим . Общее решение этого уравнения будем искать в виде произведения двух функций .

Уравнение примет вид , или

. (*)

Решаем в следующем порядке.

1. Функцию v следует взять так, чтобы .

Решим это уравнение:

или v=х;

2. Найдем функцию u, для этого подставим в уравнение (*) вместо v=х.

Получим .

3. Общее решение исходного уравнения имеет следующий вид:

.

4. Для того чтобы найти частное решение, удовлетворявшее данным начальным условиям, нужно в общее решение подставить и . Получим 0=1(е+с), отсюда с =-е.

Итак, частное решение имеет вид .

Задача 2. Найти общее решение дифференциального уравнения

и частное решение, удовлетворяющее начальному условию при .

Решение. Это однородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Составим характеристическое уравнение и решим его.

.

Тогда общее решение данного уравнения будет иметь вид

,

т.е. .

Найдем частное решение, для этого найдем у'.

.

Подставим в общее решение и в его производную данные начальные условия. Получим систему двух уравнений с неизвестными .

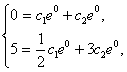или

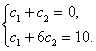
Получим . Итак, частное решение имеет вид

.