Таблица интегралов

Интегральное исчисление

Задача 1. Найти неопределенный интеграл  .

Решение. Это интеграл от алгебраической суммы функций.

Применяя свойства интеграла, получим:

Проверим результат дифференцированием:

.

 

Задача 2. Найти неопределенный интеграл  .

Решение. Аналогично предыдущему примеру:

.

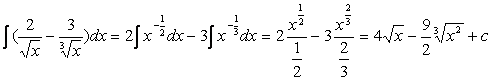Проверка. Продифференцируем полученное выражение:

.

Задача 3. Найти неопределенный интеграл  .

Решение. Преобразуем дифференциал.

.

 

Задача 4. Найти неопределенный интеграл  .

Решение. Преобразуем дифференциал.

.

 

Задача 5. Найти неопределенный интеграл  .

Решение. Преобразуем дифференциал.

.

 

Задача 6. Найти неопределенный интеграл  .

Решение. Представим подынтегральную функцию в виде суммы целой рациональной функции и правильной дроби:

.

Тогда

 

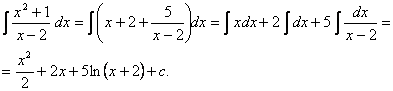
Задача 7. Найти неопределенный интеграл  .

Решение. Найдем . Тогда

 

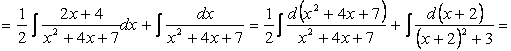
Задача 8. Найти неопределенный интеграл  .

Решение. Обозначим , тогда .

Интеграл примет вид

 

Задача 9. Найти неопределенный интеграл  .

Решение. Имеем случай четных степеней, поэтому подынтегральное выражение преобразуем по формулам понижения степеней.

.

 

Задача 10. Найти неопределенный интеграл 

Решение. Здесь косинус в нечетной степени, поэтому можно свести интеграл к степенному интегралу:

 

 

Задача 11. Найти неопределенные интеграл 

Решение. Используем метод интегрирования по частям.

Обозначим через , тогда.

Находим    и  . Тогда

.

 

Задача 12. Найти неопределенный интеграл  .

Решение. Используем метод интегрирования по частям.

Положим u=х , тогда du=.

Находим    ,   .  Тогда

 

Задача 13. Вычислить определенный интеграл .

Решение.

.

 

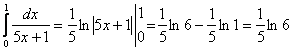Задача 14. Вычислить определенный интеграл  .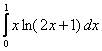

Решение. Примем за , тогда  .

Найдем  , . Тогда

 

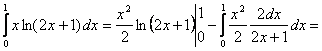
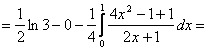
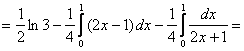
Задача 15. Вычислить определенный интеграл  .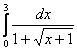

Решение. Пусть , тогда , .

Если х=0, то , если х=3, то . Тогда

.

 

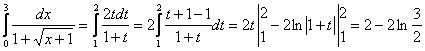Задача 16. Исследовать несобственный интеграл  на  сходимость и найти его значение в случае сходимости.

Решение. Промежуток интегрирования не ограничен, следовательно, это несобственный интеграл первого рода.

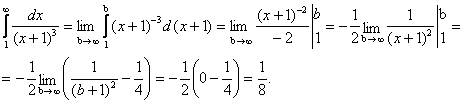
Несобственный интеграл сходится и равен 1/8.

 

Задача 17. Исследовать несобственный интеграл  на сходимость и найти его значение в случае сходимости.

Решение. Функция не ограничена на промежутке интегрирования, следовательно, это несобственный интеграл второго рода.

Несобственный интеграл сходится и равен .

 

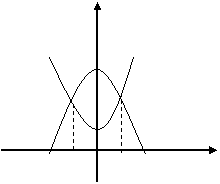
Задача 18. Найти площадь фигуры, ограниченной линиями  .

Решение. Построим данные параболы.

 

                                                                                                  

                                             Y                                                   

                                                                                                 

                                                                                                  

                                               3                              

                                                                                                  

                                               1                                                 

                                                                                

                                   -2  -1  0        1    2                 X               

 

Найдем абсциссы точек пересечения. Для этого решим систему

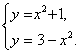
Получим  х1 = -1,  х2 =1.

Фигура ограничена графиками двух функций, следовательно, площадь ее находится по формуле

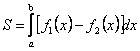,  где  . Тогда

.

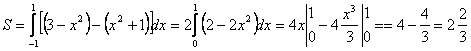Ответ: .

 

Задача 19. Вычислить объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями: .

 

Решение. Сделаем чертеж.

                                                                                                    

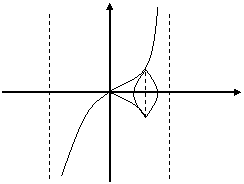                                                Y                y=tgx                          

                                                                                                    

                                                                                                    

                                                                                                    

                                                                                                    

                              -p/2                                p/2          X             

                                                        p/4                                      

                                                                                                    

                                                                                                    

                                                                                                    

 

Так как вращение фигуры происходит вокруг оси ОХ, то объем тела определяем по формуле 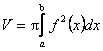, где а=0, b=, f(x)=tgx.

.

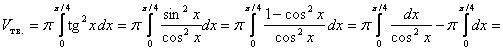
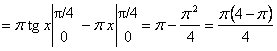Ответ: .