Теория пределов

Задача 1. Найти .

Решение. Так как пределы числителя и знаменателя существуют и предел знаменателя не равен нулю, то можно применить теорему о пределе дроби:

.

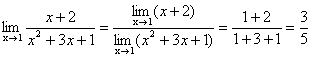Задача 2. Найти .

Решение. Имеем неопределенность вида . Для раскрытия этой неопределенности преобразуем дробь, разложив числитель и знаменатель на множители. Для значения имеем тождество

.

Поэтому пределы этих функций равны между собой:

.

Задача 3. Найти .

Решение. Непосредственная подстановка приводит к неопределенности вида . Для того чтобы раскрыть эту неопределенность, выделим множитель в числителе и в знаменателе. Для этого умножим числитель и знаменатель дроби на выражения, сопряженные, соответственно, числителю и знаменателю:

.

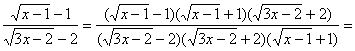
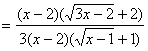Тогда

.

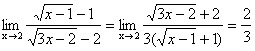Задача 4. Найти .

Решение. Здесь также непосредственно теорему о пределе дроби применить нельзя, так как числитель и знаменатель дроби при не имеют конечных пределов. Это неопределенность вида . Для раскрытия ее разделим числитель и знаменатель на х в высшей степени, т.е. на , и затем перейдем к пределу.

.

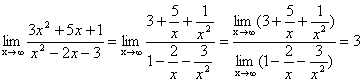Здесь - бесконечно малые функции при , и поэтому их пределы равны нулю.

Задача 5. Найти .

Решение. Имеем неопределенность вида . Воспользуемся первым замечательным пределом.

.

Можно привести другое решение.

Пусть , тогда при . Тогда

.

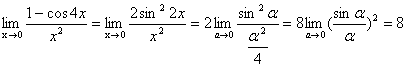Задача 6. Найти .

Решение. Здесь имеем неопределенность вида . Для раскрытия этой неопределенности преобразуем функцию так, чтобы можно было воспользоваться вторым замечательным пределом.

.

Введем новую переменную. Пусть , тогда , при , . Следовательно:

.