Многочлены

Определение 1. Функция , где n - натуральное число, - комплексные числа, называется многочленом (полиномом) степени n. Независимая переменная принимает комплексные значения.

Определение 2. Корнем многочлена называют значение переменной , при которой он обращается в ноль:

.

Теорема 1. (Безу). При делении многочлена на разность получается остаток, равный .

Следствие. Если - корень многочлена, то делится на без остатка.

.

Теорема 2. (основная теорема алгебры). Всякий многочлен степени не меньше единицы имеет, по крайней мере, один комплексный корень.

Теорема 3. Всякий многочлен -й степени разлагается на линейных множителей вида и множитель, равный коэффициенту при :

.

Следствие. Многочлен -й степени не может иметь более чем различных корней.

Теорема 4. Если значения двух многочленов и -й степени совпадают при различных значениях аргумента х, то эти многочлены совпадают в любой точке.

Теорема 5. Если два многочлена равны в любой точке, то их коэффициенты совпадают.

Определение 3. Если в разложении многочлена степени не выше

,

некоторые множители окажутся одинаковыми, т.е.

,

,

то называется корнем кратности , - кратности и т.д.

Теорема 6. Если является корнем многочлена кратности , то для производной это число является корнем кратности .

Следствие. Число является корнем кратности для , …, корнем кратности 1 для .

Теорема 7. Если многочлен с действительными коэффициентами имеет корень , то он имеет сопряженный корень .

Следствие. В разложение комплексные корни входят попарно сопряженными.

Если комплексное число является корнем кратности , то и сопряженное число является корнем кратности .

Многочлен с действительными коэффициентами разлагается на множители с действительными коэффициентами первой и второй степеней соответствующей кратности:

,

.

Определение 4. Функция называется рациональной, если ее можно представить в виде дроби

,

где P(x) и Q(x) - многочлены.

Из класса всех дробей выделяют основные простые дроби:

,

где a, p ,q, А M, N Î R ; m, kÎ N, квадратный трехчлен не имеет действительных корней.

Если степень числителя не ниже степени знаменателя, то дробь называется неправильной; в таком случае, выполнив деление, получим

,

где W(х) - некоторый многочлен, а второе слагаемое представляет собой правильную дробь, у которой степень числителя меньше степени знаменателя.

Теорема 8. Каждый многочлен Q(x) с действительными коэффициентами может быть представлен единственным образом в виде

,(1)

где … - корни многочлена кратности k, l, …; квадратичные множители кратности m, n, … не имеют действительных корней.

Теорема 9. Пусть R(x)/Q(x) - правильная рациональная дробь, у которой знаменатель представлен в виде (1). Тогда указанную дробь можно единственным образом представить в виде суммы простых дробей:

(2)

где - некоторые действительные числа.

Выражение (2) называется разложением рациональной дроби на простые дроби, числа - коэффициентами разложения.

Следствие. Пусть R(x)/Q(x) - правильная рациональная дробь, у которой знаменатель многочлен степени n, имеющий n различных действительных корней . Тогда эту дробь можно единственным образом представить в виде суммы простых дробей:

, (3)

где - некоторые действительные числа.

Для определения коэффициентов разложения используют метод неопределенных коэффициентов, который состоит в следующем: приводят левую часть равенства (2) или (3) к общему знаменателю и приравнивают коэффициенты при одинаковых степенях многочлена, полученного в числителе, и многочлена R(x).

Интерполяционная формула Лагранжа

На отрезке заданы значения неизвестной функции в различных точках:

				.

Требуется найти многочлен степени не выше , приближенно выражающий функцию . В качестве такого многочлена можно взять многочлен, значения которого в точках совпадают с . Данная задача является задачей интерполирования функции.

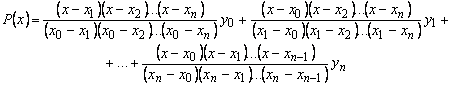
- интерполяционная формула Лагранжа.