Комплексные
числа
Комплексные числа являются расширением
множества действительных чисел R.
Определение 1. Выражение вида ![]() , где a, bÎ R, i - мнимая единица, определяемая равенствами
, где a, bÎ R, i - мнимая единица, определяемая равенствами ![]() ,
, ![]() , называется комплексным числом, при этом
, называется комплексным числом, при этом ![]() называется действительной (вещественной)
частью комплексного числа z (a = Re z); b называется мнимой частью комплексного числа z (b =
Im z).
называется действительной (вещественной)
частью комплексного числа z (a = Re z); b называется мнимой частью комплексного числа z (b =
Im z).
Множество комплексных чисел обозначается
буквой C, R Ì C. Два числа ![]() и
и ![]() считаются равными,
если
считаются равными,
если ![]() ,
, ![]() или Re z1=Re z2, Im z1=Im z2.
или Re z1=Re z2, Im z1=Im z2.
Каждому комплексному числу
из множества C можно поставить в
соответствие точку координатной плоскости (рис. 1). Числу ![]() соответствует точка
соответствует точка ![]() . Вектор
. Вектор ![]() считают
геометрическим изображением комплексного числа, а всю плоскость - комплексной
плоскостью.
считают
геометрическим изображением комплексного числа, а всю плоскость - комплексной
плоскостью.
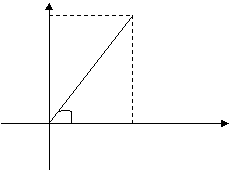
Im z A (a,b)
r
φ C
О а
Re z
Рис. 1
Обозначим длину вектора ![]() . Угол, который вектор
. Угол, который вектор ![]() образует с
положительным направлением оси Re z, обозначим
образует с
положительным направлением оси Re z, обозначим
![]() . Из DАСО:
. Из DАСО:
Re z = ![]() , Im z =
, Im z =
![]() ,
,
![]()
- тригонометрическая форма записи комплексного числа.
Определение 2. Величина ![]() называется модулем
комплексного числа.
называется модулем
комплексного числа.
Определение 3. Угол, который вектор ![]() образует с
положительным направлением оси Re z, называется аргументом комплексного числа
образует с
положительным направлением оси Re z, называется аргументом комплексного числа
![]()
![]() .
.
Определение 4. Суммой (разностью) двух комплексных чисел ![]() и
и ![]() называется комплексное
число
называется комплексное
число ![]() , определяемое равенством
, определяемое равенством ![]() .
.
Re z = Re z1![]() Re z2, Im z = Im z1
Re z2, Im z = Im z1![]() Im z2.
Im z2.
Определение 5. Произведением комплексных чисел ![]() и
и ![]() называется комплексное
число, которое получится, если перемножить эти числа как двучлены по правилам
алгебры.
называется комплексное
число, которое получится, если перемножить эти числа как двучлены по правилам
алгебры.
![]()
Re z = а1а2–b1b2, Im z = a1b2 + a2b1.
Если комплексные числа записаны в
тригонометрической форме
![]() ,
, ![]() ,
,
![]()
![]() ,
,
![]() .
.
![]() ,
, ![]() .
.
При перемножении комплексных
чисел модуль произведения равен произведению модулей, а аргумент равен сумме
аргументов.
Определение 6.
Комплексные числа ![]() и
и ![]() называются
сопряженными.
называются
сопряженными.
Сопряженные числа обладают следующими свойствами:
![]() ,
,
![]() .
.
Произведение сопряженных чисел
равно квадрату модуля каждого из них.
Чтобы разделить комплексное число z1 на комплексное число z2, надо умножить
делимое и делитель на сопряженное делителю комплексное число. Тогда в
знаменателе дроби получится действительное число.
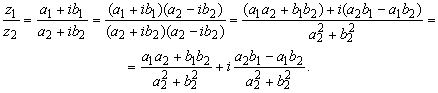
Формула для деления комплексных чисел, заданных в
тригонометрической форме:
![]() .
.
Из формулы для произведения комплексных чисел следует формула Муавра: если ![]() , то
, то ![]() .
.
При возведении комплексного
числа в натуральную степень модуль возводится в эту степень, а аргумент
умножается на нее.
![]() ,
, ![]() .
.
Корнем n-й степени (nÎ N) из комплексного числа называется комплексное число, n-я степень
которого равна подкоренному числу.
![]() .
.
Меняя ![]() , мы получим n
различных значений корня из комплексного
числа. Следовательно, корень n-й степени из
действительного числа также имеет n комплексных
значений, так как действительное число является частным случаем комплексного
числа.
, мы получим n
различных значений корня из комплексного
числа. Следовательно, корень n-й степени из
действительного числа также имеет n комплексных
значений, так как действительное число является частным случаем комплексного
числа.
Пусть z=a+ib комплексное число. Его можно представить в
показательной форме ![]() , где r =½z½, j=Arg z.
, где r =½z½, j=Arg z.