Линейные преобразования и квадратичные формы

Линейное преобразование и его матрица

Пусть V - линейное пространство. Если каждому вектору из по некоторому правилу ставится в соответствие единственный вектор из V, то будем говорить, что задано преобразование пространства f.

Преобразование f называется линейным, если для любых векторов и для любого выполняются равенства , .

Если пространство имеет размерность и - какой-либо базис в нем, то связь между координатами вектора и его образа в выбранном базисе в матричной форме имеет вид

,

где , ,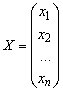

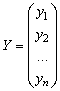- квадратная матрица порядка , -й столбец которой составлен из координат вектора в базисе (матрица А называется матрицей линейного преобразования f в выбранном базисе).

Произведение линейных преобразований

Если и два линейных преобразования в пространстве , то возможно умножение линейных преобразований в том или ином порядке. Произведение линейных преобразований также является линейным преобразованием.

Характеристическое уравнение

линейного преобразования

Характеристическим многочленом преобразования или матрицы А называется многочлен -й степени относительно , имеющий вид , где - единичная матрица порядка .

Характеристическим уравнением линейного преобразования f или матрицы А называется уравнение

,

где - матрица этого преобразования в некотором базисе, а его корни называются собственными числами линейного преобразования, а также матрицы .

Собственные векторы линейного преобразования

Ненулевой вектор линейного пространства называется собственным вектором линейного преобразования , если существует такое вещественное число , что выполняется равенство

. (1)

Число называется собственным значением преобразования , или собственным числом вектора относительно преобразования . Равенство (1) можно записать в матричном виде:

, (2)

где - матрица преобразования в некотором базисе;

- матрица-столбец из координат вектора в этом базисе.

Ненулевую матрицу-столбец удовлетворяющую условию (2), называют собственным вектором-столбцом матрицы с собственным значением .

Отыскание собственных векторов

линейного преобразования

Собственные значения линейного преобразования (матрицы ) являются его (ее) вещественными характеристическими числами, т.е. вещественными корнями уравнения (9.4). Сами же собственные векторы отыскиваются из матричного уравнения или из системы линейных однородных уравнений

Ортогональные матрицы и преобразования

При изучении линейных преобразований евклидова пространства полезно использовать ортогональные матрицы. Матрица называется ортогональной, если транспонированная матрица совпадает с обратной.

Диагональная матрица может быть ортогональной лишь в том случае, если ее диагональные элементы равны . Для ортогональной матрицы определитель равен .

Например, ортогональными являются следующие матрицы:

, , .

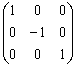Линейное преобразование евклидова пространства называется ортогональным, если его матрица в некотором ортонормированном базисе является ортогональной. Базис называется ортонормированным, если длины векторов равны единице и вектора попарно ортогональны.

Симметрические матрицы и преобразования

Матрица называется симметрической, если ее элементы, симметричные относительно главной диагонали, равны между собой, т.е. .

Например, матрица

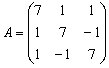
является симметрической.

Линейное преобразование евклидова пространства называется симметрическим, если для произвольных векторов и скалярное произведение равно скалярному произведению .

В любом ортонормированном базисе матрица симметрического преобразования является симметрической.

Произвольную симметрическую матрицу можно привести к диагональному виду с помощью ортогональной матрицы.

Любое симметрическое линейное преобразование (с матрицей ) в пространстве имеет, по крайней мере, одну тройку попарно перпендикулярных собственных векторов, при определении которых возможны следующие случаи.

1. Если собственные значения симметрической матрицы различны, то соответствующие собственные векторы попарно ортогональны.

2. Если среди чисел два одинаковых, то двукратному корню, например , соответствует бесконечное множество собственных векторов, лежащих в плоскости, перпендикулярной к собственному вектору , соответствующему собственному значению .

3. Если все собственные значения одинаковы, т.е. - трехкратный корень характеристического уравнения, то симметрическое линейное преобразование есть преобразование подобия пространства с коэффициентом подобия . Следовательно, в этом случае любые три попарно перпендикулярных вектора являются собственными векторами симметрического преобразования .

Квадратичные формы и приведение

их к каноническому виду

Квадратичной формой от переменных называется симметрический однородный многочлен второй степени от этих переменных

, (3)

где .

Если ввести матрицу из коэффициентов квадратичной формы (3)

и матрицу-столбец из переменных

,

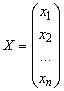то, пользуясь правилом умножения матриц, квадратичную форму (3) можно записать в матричном виде

.

Привести квадратичную форму (9.8) к каноническому виду - значит представить ее следующим образом:

. (4)

Матрица В, соответствующая квадратичной форме (4), диагональна.

Так как матрица симметрическая вещественная, задача приведения к каноническому виду квадратичной формы (3) сводится к задаче приведения к диагональному виду матрицы симметрического линейного преобразования с помощью ортогональной матрицы (ортогонального преобразования).

Корни характеристического уравнения матрицы называют характеристическими числами квадратичной формы (3), а направления собственных векторов, соответствующих характеристическим числам, главными направлениями квадратичной формы.

Правило нахождения ортогонального преобразования, приводящего квадратичную форму переменных к каноническому виду:

1) записать квадратичную форму в симметрическом виде;

2) записать матрицу квадратичной формы;

3) составить характеристическое уравнение ;

4) найти собственные значения ;

5) записать однородную систему уравнений и найти собственные векторы матрицы ;

6) образовать новый ортогональный базис из собственных векторов и составить ортогональную матрицу перехода ;

7) записать канонический вид квадратичной формы.