Системы линейных однородных уравнений.

Фундаментальная система решений

Система линейных уравнений называется однородной, если все свободные члены уравнений равны нулю:

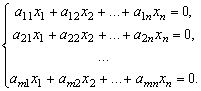
Однородная система всегда совместна, поскольку она всегда имеет тривиальное (нулевое) решение. Однако наибольший интерес представляют нетривиальные решения.

Теорема 1. Однородная система линейных уравнений имеет нетривиальное решение тогда и только тогда, когда ранг матрицы системы меньше числа неизвестных: r(A)=r<n.

Справедливо следующее утверждение: линейная комбинация решений однородной системы линейных уравнений также является ее решением.

Максимальная линейно независимая система решений называется фундаментальной системой решений однородной системы уравнений. Фундаментальная система решений содержит (n-r) векторов. Любое решение системы может быть представлено в виде линейной комбинации векторов фундаментальной системы решений.

Для нахождения фундаментальной системы решений нужно:

1) r базисных переменных выразить через свободные переменные;

2) выбрать линейно независимую систему (n-r) векторов (n-r)-мерного пространства (например, это могут быть единичные векторы);

3) поочередно заменить свободные переменные координатами векторов выбранной системы и вычислить значения базисных переменных.

Полученные решения ,, …, образуют фундаментальную систему решений. Тогда общее решение однородной системы уравнений имеет вид

,

где - произвольные числа.