Системы линейных неравенств
Пример 1. Решить систему линейных неравенств
графически и найти угловые точки множества решений. Записать формулу для
граничных точек.
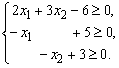
Решение. Найдем полуплоскость, в которой выполняется первое неравенство
системы. Для этого проведем прямую ![]() (на рис. 9.1 это
прямая
(на рис. 9.1 это
прямая ![]() ).
).
Представим неравенство в виде
![]()
и получим решение первого неравенства системы в
полуплоскости, расположенной справа от прямой ![]() . Убедиться, что выбрана нужная полуплоскость, можно,
подставив в неравенство координаты произвольной точки плоскости, не лежащей на
прямой
. Убедиться, что выбрана нужная полуплоскость, можно,
подставив в неравенство координаты произвольной точки плоскости, не лежащей на
прямой ![]() . Например, для точки О(0; 0) неравенство не выполняется, следовательно,
полуплоскость слева от прямой
. Например, для точки О(0; 0) неравенство не выполняется, следовательно,
полуплоскость слева от прямой
![]() не является решением -
решение "справа". Аналогично решаем второе и третье неравенства и
находим пересечение полученных полуплоскостей (рис. 1).
не является решением -
решение "справа". Аналогично решаем второе и третье неравенства и
находим пересечение полученных полуплоскостей (рис. 1).
 X2
X2
A
3 B (l3)
2
X1
O 3
5
C (l1)
(l2)
Рис. 1
Решением системы неравенств
является многогранник (в данном случае треугольник) с вершинами А, В, С.
Для нахождения координат вершин решим соответствующие системы уравнений:
А: ![]()
![]() ;
;
В: ![]()
![]() ;
;
С: ![]()
![]() .
.
Точки А, В и С - угловые точки.
Граничными точками являются точки отрезков
![]() ,
, ![]() и
и ![]() . Множество точек отрезка
. Множество точек отрезка ![]() является выпуклой
линейной оболочкой
является выпуклой
линейной оболочкой ![]() и
и ![]() , поэтому для любой точки
, поэтому для любой точки ![]() отрезка
отрезка ![]() получим
получим
![]() .
.
Подставляем в данное равенство координаты
точек ![]() и
и ![]() .
.

Аналогично получаем формулы граничных
точек отрезков ![]() и
и ![]() :
:
![]()
![]() .
.
Пример 2. Решить
систему линейных неравенств и найти угловые точки:
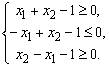
Решение. Проводим прямые, выбираем нужные полуплоскости и
находим их пересечение:
 X2
X2
A
O 1 X1
B
Искомое решение -
многогранная область с вершинами А(0; 1) и В(1; 0).
Пример 3. Решить
систему линейных неравенств
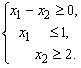
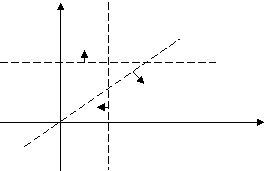
Решение. Проводим прямые, выбираем нужные полуплоскости
(рис. 2).
 X2
X2
2
O
1 X1
Рис. 2
Так как точек, общих для
всех трех выбранных полуплоскостей, нет, система несовместна.
Пример 4. Найти область неотрицательных решений системы линейных
неравенств и угловые точки этой области:
![]()
Решение.
Нахождение неотрицательных
значений обеспечивается выполнением дополнительных ограничений
![]()
даже если они не
указаны в системе. Таким образом, пример решается аналогично предыдущим с
учетом этих двух дополнительных неравенств (рис. 3).
 X2
X2
2 A
B
O
C X1
-2
Рис. 3
Искомым решением является четырехугольник ОАВС с угловыми точками О(0; 0), А(0; 2), В(2; 2), С(1; 0).