Линейные преобразования и квадратичные формы
Пример 1. Пусть в двухмерном пространстве линейное
преобразование ![]() в базисе
в базисе ![]() задано матрицей
задано матрицей
![]() .
.
Найти ![]() , если
, если ![]() .
.
Решение.
По формуле ![]()
![]() .
.
Следовательно, ![]() .
.
Пример 2. Даны два линейных преобразования:
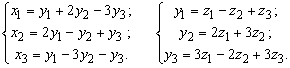
Найти линейное преобразование, выражающее ![]() через
через
![]() .
.
Решение. Обозначим первое преобразование ![]() , а второе
, а второе ![]() и их матрицы
и их матрицы ![]() и В, соответственно. Тогда искомое
преобразование есть
и В, соответственно. Тогда искомое
преобразование есть ![]() и его матрица
и его матрица
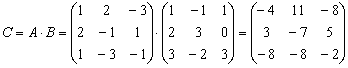 ,
,
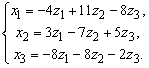
Пример 3. Найти
характеристический многочлен и характеристические числа матрицы
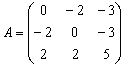 .
.
Решение. Характеристический многочлен
данной матрицы имеет вид
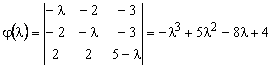 .
.
Для нахождения характеристических чисел
решаем уравнение
![]() .
.
![]()
![]()
![]()
Корни данного уравнения
(характеристические числа): ![]() .
.
Пример 4. Пусть
линейное преобразование ![]() линейного двухмерного
пространства в базисе
линейного двухмерного
пространства в базисе ![]() имеет матрицу
имеет матрицу ![]() . Доказать, что вектор
. Доказать, что вектор ![]() является собственным
вектором этого преобразования с собственным числом
является собственным
вектором этого преобразования с собственным числом ![]() .
.
Решение. Вектор ![]() ненулевой и
ненулевой и
![]()
т.е. ![]() .
.
Пример 5. Найти
собственные значения и собственные векторы преобразования ![]() , заданного в некотором базисе матрицей
, заданного в некотором базисе матрицей
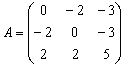 .
.
Решение. Характеристическое уравнение имеет вид ![]() , и так как его корни
, и так как его корни ![]() характеристические
числа, то они являются собственными значениями
характеристические
числа, то они являются собственными значениями ![]() . Собственные векторы, соответствующие собственным значениям
. Собственные векторы, соответствующие собственным значениям ![]() и
и ![]() , найдем из системы (9.7), которая в данном случае примет вид
, найдем из системы (9.7), которая в данном случае примет вид
 или
или 
Подставив сюда ![]() , получим систему уравнений
, получим систему уравнений
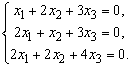
Ранг матрицы данной системы равен 2; одно
из ее решений имеет вид ![]() ;
; ![]() ;
; ![]() . Тогда собственные векторы для
. Тогда собственные векторы для ![]() имеют вид
имеют вид ![]() , где
, где ![]() - любое действительное число.
- любое действительное число.
Пусть теперь ![]() , тогда
, тогда
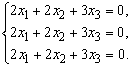
Ранг полученной системы уравнений равен 1.
Два ее линейно независимых решения имеют следующий вид:
![]() ;
;
![]() .
.
Собственные векторы для
![]() имеют вид
имеют вид ![]() и
и ![]() , где
, где ![]() и
и ![]() - любые действительные числа.
- любые действительные числа.
Пример 6. Найти
собственные значения и собственные векторы симметрического линейного
преобразования, заданного в некотором ортогональном базисе матрицей
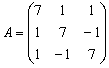
и привести ее к диагональному виду.
Решение. Составим характеристическое уравнение
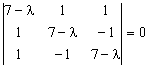
или
![]() .
.
Корни указанного уравнения: ![]() .
.
Собственные векторы, соответствующие ![]() и
и ![]() , найдем из системы (9.7), которая для данного примера примет
вид
, найдем из системы (9.7), которая для данного примера примет
вид
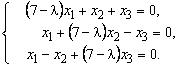
Подставив сюда ![]() , получим
, получим
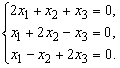
Ранг приведенной системы равен 2. Одно из
решений данной системы: ![]() ,
, ![]() ,
, ![]() . Тогда собственные векторы для
. Тогда собственные векторы для ![]() имеют вид
имеют вид ![]() , где
, где ![]() - любое действительное число.
- любое действительное число.
Аналогично найдем собственные векторы с
собственным значением ![]() :
:
![]() ,
,
где ![]() - любое действительное число.
- любое действительное число.
Так как собственное значение ![]() является двукратным
корнем характеристического уравнения, ему соответствует бесконечное множество
собственных векторов, лежащих в плоскости, перпендикулярной к собственному
вектору, соответствующему собственному значению
является двукратным
корнем характеристического уравнения, ему соответствует бесконечное множество
собственных векторов, лежащих в плоскости, перпендикулярной к собственному
вектору, соответствующему собственному значению ![]() . Поэтому, умножив векторно
. Поэтому, умножив векторно ![]() на
на
![]() , найдем еще собственные векторы с
собственным значением
, найдем еще собственные векторы с
собственным значением ![]() :
:
![]() .
.
Итак, симметрическое
линейное преобразование с данной симметрической матрицей ![]() имеет, по крайней
мере, одну тройку попарно перпендикулярных собственных векторов, а следовательно, матрицу
имеет, по крайней
мере, одну тройку попарно перпендикулярных собственных векторов, а следовательно, матрицу ![]() можно привести к
диагональному виду с помощью ортогональной матрицы.
можно привести к
диагональному виду с помощью ортогональной матрицы.
Нормируя ортогональные собственные векторы
![]() ,
, ![]() и
и ![]() , получаем векторы
, получаем векторы
![]() ,
, ![]() и
и ![]() ,
,
которые составляют ортонормированный базис.
Ортогональная матрица перехода ![]() имеет вид
имеет вид
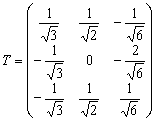 .
.
Обратная ей матрица
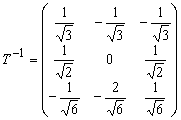 .
.
Тогда ![]() .
. 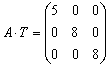 - диагональная
матрица, элементами главной диагонали которой являются собственные значения.
- диагональная
матрица, элементами главной диагонали которой являются собственные значения.
Пример 7. Привести к каноническому виду
квадратичную форму:
![]() .
.
Решение.
1) Запишем квадратичную форму в
симметрическом виде:
![]() ;
;
2) запишем матрицу ![]() квадратичной формы:
квадратичной формы:
![]() ;
;
3) составим характеристическое уравнение
матрицы ![]() :
:
![]() ,
,
или
![]() ;
;
4) находим ![]() - собственные значения матрицы
- собственные значения матрицы ![]()
5) запишем систему уравнений, определяющих
искомые собственные векторы:
![]()
Подставляя сюда ![]() и
и ![]() , найдем собственные векторы
, найдем собственные векторы ![]() и
и ![]() . Заметим, что они ортогональны;
. Заметим, что они ортогональны;
6) нормируя ортогональные собственные
векторы ![]() и
и ![]() , находим векторы, образующие новый ортонормированный базис и
определяющие главные направления квадратичной формы:
, находим векторы, образующие новый ортонормированный базис и
определяющие главные направления квадратичной формы:
![]() .
.
Ортогональная матрица перехода ![]() имеет вид
имеет вид
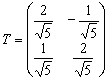 ;
;
7) матрица ![]() , обратная матрице
, обратная матрице ![]() , имеет вид
, имеет вид
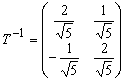 ,
,
тогда ![]() - диагональный вид матрицы
- диагональный вид матрицы ![]() в найденном
ортонормированном базисе.
в найденном
ортонормированном базисе.
Итак, ортогональное преобразование
переменных
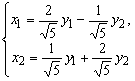
приводит данную квадратичную форму к каноническому
виду (в чем можно убедиться, непосредственно произведя вычисления):
![]() .
.
Пример 8. Привести к каноническому виду квадратичную форму
![]() .
.
Решение.
![]() .
.
Матрица квадратичной формы имеет вид
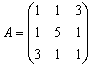 ,
,
а характеристическое уравнение
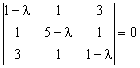 ,
,
или
![]() ,
,
![]() ,
,
откуда ![]() , следовательно, канонический вид квадратичной формы:
, следовательно, канонический вид квадратичной формы:
![]() .
.
Найдем базис, в котором квадратичная форма
имеет такой вид. Система уравнений для отыскания собственных векторов имеет вид
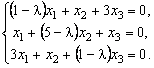
При ![]() из системы
из системы
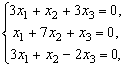
имеющей ранг 2, находим собственный вектор ![]() .
.
При ![]() из системы
из системы
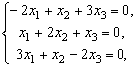
имеющей ранг 2, находим собственный вектор ![]() .
.
При ![]() из системы
из системы
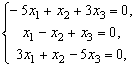
имеющей ранг 2, находим собственный вектор ![]() .
.
Полученные векторы ![]() попарно ортогональны. Нормируя их, находим векторы
попарно ортогональны. Нормируя их, находим векторы
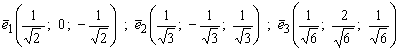 ,
,
образующие ортогональный базис и определяющие главные
направления квадратичной формы.
Ортогональная матрица ![]() имеет вид
имеет вид
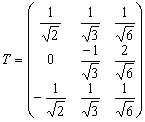 .
.
Итак, ортогональные преобразования
переменных
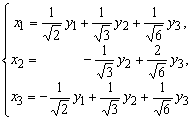
приводят заданную квадратичную форму к каноническому
виду:
![]() .
.