Системы линейных однородных уравнений.

Фундаментальная система решений

Пример. Найти фундаментальную систему решений системы уравнений

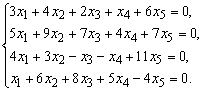
Решение. Выпишем матрицу системы и с помощью элементарных преобразований приведем ее к треугольному виду:

.

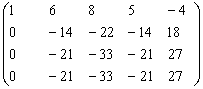
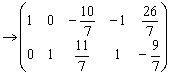Ранг матрицы r = r(A)=2. Число неизвестных n = 5. Следовательно, в фундаментальную систему решений войдут n - r = 5 - 2 = 3 вектора: ,,.

Выберем в качестве базисных переменных и и выразим их через свободные переменные:

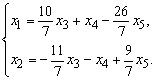
Заменим свободные переменные координатами трехмерных единичных векторов: (1; 0; 0), (0; 1; 0), (0; 0; 1).

Пусть . Тогда . Полученная совокупность неизвестных составляет решение

.

При базисные переменные . Полученная совокупность неизвестных составляет решение

.

Аналогично для находим решение

.

Векторы ,, образуют фундаментальную систему решений.