Решение произвольных систем
линейных уравнений
Пример 1. Решить систему линейных уравнений
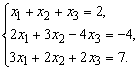
Решение. Выпишем расширенную матрицу системы:
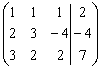
![]() .
.
Выполняя элементарные преобразования, приведем левую
часть матрицы к единичному виду: на главной диагонали будем создавать единицы,
а вне ее - нули.
Создадим нули в первом столбце. Для этого
первую строку перепишем, а затем, умножив ее на –2 и –3, прибавим ко второй и
третьей строкам, соответственно:
![]()
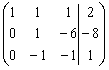
![]()
Создадим нули во втором столбце. Для этого
вторую строку перепишем, а затем сложим с третьей строкой и, умножив на (–1),
сложим с первой строкой.
![]()
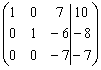
![]()
Разделим третью строку на –7, создав таким
образом единицу на диагонали:
![]()
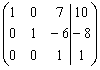
![]()
Создадим нули в третьем столбце. Для этого
третью строку перепишем, а затем, умножив ее на 6 и на –7, сложим со второй и
третьей строками, соответственно:
![]()
 .
.
![]() Итак, левая часть матрицы приведена к диагональному виду. Полученная
матрица соответствует системе уравнений
Итак, левая часть матрицы приведена к диагональному виду. Полученная
матрица соответствует системе уравнений 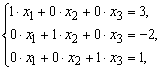 или
или 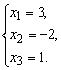
Пример 2.
Найти общее и базисное решения системы
уравнений
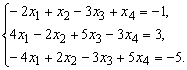
Решение. Составим расширенную матрицу системы:
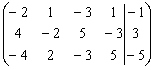 .
.
Выберем первую базисную переменную. Столбец коэффициентов
при ней будет приведен к виду ![]() , т.е. эта переменная будет исключена из всех уравнений, кроме
первого. Пусть, например, это будет переменная
, т.е. эта переменная будет исключена из всех уравнений, кроме
первого. Пусть, например, это будет переменная ![]() (это удобно, так как
во втором столбце есть единица в первой строке).
(это удобно, так как
во втором столбце есть единица в первой строке).
Для исключения базисной переменной ![]() первую строку
перепишем, а во второй и третьей строках второго столбца создадим нули:
первую строку
перепишем, а во второй и третьей строках второго столбца создадим нули:
 .
.
Выберем вторую базисную переменную.
Столбец коэффициентов при ней будет приведен к виду ![]() , т.е. эта переменная будет исключена из всех уравнений, кроме
второго. Пусть это будет переменная
, т.е. эта переменная будет исключена из всех уравнений, кроме
второго. Пусть это будет переменная ![]() .
.
Для исключения базисной переменной ![]() умножим вторую строку
на –1, а затем в первой и третьей строках создадим нули в третьем столбце:
умножим вторую строку
на –1, а затем в первой и третьей строках создадим нули в третьем столбце:

![]()

![]()
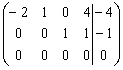 .
.
Отбросим нулевую строку:
![]() .
.
Итак, количество базисных переменных равно
рангу матрицы. Переменные ![]() и
и ![]() введены в базис.
введены в базис.
Выпишем систему уравнений,
соответствующую полученной матрице:
![]()
Преобразуем данную систему, оставив в левых частях
уравнений только базисные переменные:
![]()
Полученная зависимость базисных переменных
![]() и
и ![]() от свободных
переменных
от свободных
переменных ![]() и
и ![]() и есть общее решение исходной системы уравнений.
и есть общее решение исходной системы уравнений.
Для того чтобы найти базисное решение,
нужно свободным переменным ![]() и
и ![]() придать нулевые
значения и вычислить значения базисных переменных
придать нулевые
значения и вычислить значения базисных переменных ![]() и
и ![]() :
: ![]() .
.
Пример 3.
Найти общее решение и два базисных
решения системы уравнений:
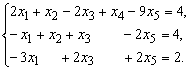
Решение.
|
Базис |
|
|
|
|
|
|
|
|
2 -1 -3 |
1
0 |
-2 1 2 |
1 0 0 |
-9 -2 2 |
4 4 2 |
|
|
3 -1 -3 |
0 1 0 |
-3 1
|
1 0 0 |
-7 -2 2 |
0 4 2 |
|
|
-1,5 0,5 -1,5 |
0 1 0 |
0 0 1 |
1 0 0 |
-4 -3 1 |
3 3 1 |
Общее решение системы :
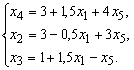
Базисное решение: ![]() .
.
Выполним переход к другому базису. Выберем
в последней таблице в качестве ключевого элемента коэффициент 1 при свободной
переменной ![]() в третьем уравнении:
переменная
в третьем уравнении:
переменная ![]() войдет в базис вместо
переменной
войдет в базис вместо
переменной ![]() .
.
|
|
-1,5 0,5 -1,5 |
0 1 0 |
0 0 1 |
1 0 0 |
-4 -3
|
3 3 1 |
|
|
-7,5 -4 -1,5 |
0 1 0 |
4 3 1 |
1 0 0 |
0 0 1 |
7 6 1 |
Второе базисное решение: ![]() .
.
Пример 4.
Найти исходное опорное решение системы
уравнений и выполнить переход к другому опорному решению:
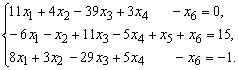
Решение.
|
базис |
|
|
|
|
|
|
|
|
|
|
11 -6 -8 |
4 -1 -3 |
-39 11 29 |
3 -5 -5 |
0 1 0 |
-1 1
|
0 15 1 |
min |
|
|
3 2 -8 |
2 -3 |
-10 -18 29 |
-2 0 -5 |
0 1 0 |
0 0 1 |
1 14 1 |
min |
|
|
-4 1 |
1 0 0 |
-10 2 -1 |
-2 4 -11 |
0 1 0 |
0 0 1 |
1 12 4 |
min
|
|
|
1 0 0 |
|
|
|
0 1 0 |
0 0 1 |
|
|
|
|
||||||||
|
|