Ряды Фурье

Рядом Фурье функции f(x), определенной на отрезке [-π, π], называется ряд

,

где

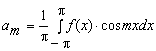(т = 0, 1, 2, …),

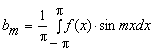(т = 1, 2, …).

Из определения следует, что сумма ряда Фурье функции f(x) является периодической функцией с периодом 2π.

Если функция f(x) задана в отрезке [–l, l], то она может быть представлена в виде суммы ряда Фурье

,

где

и .

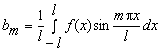Если f(x) - четная функция, то ряд Фурье содержит только свободный член и косинусы, т.е.

f(x) = ,

где

.

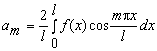Если f(x) - нечетная функция, то ряд Фурье содержит только синусы, т.е.

f(x) = ,

где

.

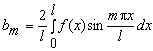Если функция f(x) задана в отрезке [0, l], то для разложения в ряд Фурье достаточно ее доопределить в отрезке [–l,0] произвольным способом, а затем разложить в ряд Фурье, считая ее заданной в отрезке [–l, l]. Наиболее целесообразно функцию достроить так, чтобы ее значения в точках отрезка [–l,0] находились из условия f(-x) = f(x) или f(-x) = -f(x). В первом случае функция f(x) в отрезке [–l, l] будет четной, а во втором случае - нечетной.