Разложение элементарных функций

в степенные ряды

Рядом Маклорена для функции называют степенной ряд вида

или в общем виде ряд

называют рядом Тейлора для функции . Для того чтобы разложить функцию в ряд Тейлора (или Маклорена), следует:

1) вычислить значение функции и ее последовательных производных в точке (или );

2) составить ряд по формуле;

3) определить область сходимости составленного степенного ряда;

4) показать, что составленный степенной ряд сходится к порождающей его функции.

Так, для наиболее распространенных элементарных функций разложение в ряд Маклорена имеет следующий вид:

;

;

;

;

.

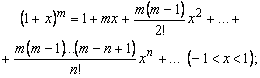
При разложении функций в ряд Маклорена или Тейлора можно использовать уже известные разложения с применением следующих свойств степенных рядов в области их сходимости:

1) два степенных ряда можно почленно складывать и умножать (по правилу умножения многочленов);

2) степенной ряд можно почленно умножать на общий множитель;

3) степенной ряд можно почленно интегрировать и дифференцировать любое число раз.