Ряды Фурье

Пример 1. Разложить в ряд Фурье функцию, заданную на отрезке [-π, π] уравнением

f(x) = π + х.

Решение. Определяем коэффициенты ряда Фурье:

.

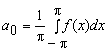
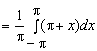
Второй интеграл равен нулю как интеграл от нечетной функции на симметричном относительно нуля промежутке. Таким образом:

+.

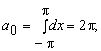
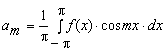
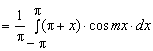
Нетрудно видеть, что оба интеграла равны нулю (подынтегральная функция второго интеграла является нечетной как произведение четной функции на нечетную):

.

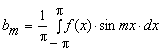
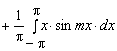Первый интеграл равен нулю (от нечетной функции по симметричному промежутку). Подынтегральная функция второго интеграла - четная функция (как произведение двух нечетных). Таким образом:

+ += =.

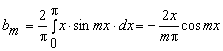
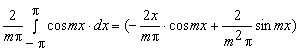
Следовательно, разложение функции f (x) = π + х в ряд Фурье имеет вид

f(x)=π + х = π + 2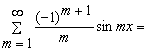

Пример 2. Разложить в ряд Фурье функцию f (x) = , заданную на полупериоде в отрезке [0, 2].

Решение. Функция может быть разложена в ряд Фурье бесчисленным количеством способов.

Рассмотрим два наиболее важных варианта разложения.

1. Доопределим функцию f (x) = на отрезке [-2; 0] четным образом.

Так как l=2, то

= ==

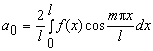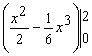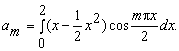
Интегрируем по частям:

= =

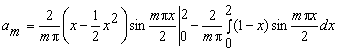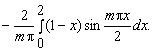
Интегрируя еще раз по частям, получаем:

+ = = = 0.

Итак:

f(x)= = =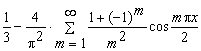

2. Доопределим функцию f(x) = на отрезке [–2; 0] нечетным образом.

Так как l = 2, то

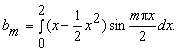
Интегрируя по частям, получаем

= =

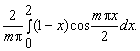
После второго интегрирования по частям имеем

+ = =

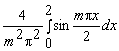= = = 0 (т = 0, 1, 2, 3,…).

Итак:

f(x) = 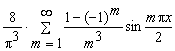= =