Вычисление объема тела вращения

Таблица интегралов

Примеры. Вычислить объем тела, образованного вращением фигуры, ограниченной линиями:

а) вокруг оси ;

б) вокруг оси .

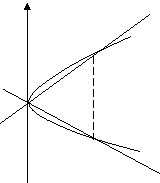
а) Решение. Найдем точки пересечения данных линий, для чего решим систему уравнений (рис. 1):

.

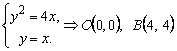Y

А

В

O X

Рис. 1

Искомый объем равен разности объемов двух тел вращения: первого, образованного вращением криволинейного треугольника , и второго, образованного вращением треугольника вокруг оси . Поэтому объем данного тела вращения составляет

.

б) Решение. Тело образовано вращением вокруг оси , поэтому

.