Интегрирование выражений,

содержащих тригонометрические функции

Интегралы видов , , вычисляют, используя тригонометрические формулы

;

;

.

При нахождении интегралов вида , где m и n - целые числа, необходимо различать следующие случаи.

1. Один из показателей m или n - нечетное положительное число. В этом случае от нечетной степени отделяют один сомножитель и вносят его под знак дифференциала, а подынтегральную функцию приводят к единой тригонометрической функции, используя тригонометрическое тождество .

2. Оба показателя m и n - четные неотрицательные числа. В этом случае подынтегральную функцию преобразуют с помощью следующих тригонометрических формул:

; ; .

3. В остальных случаях, применяя формулы тригонометрических преобразований, приводим подынтегральное выражение к описанным выше случаям.

Интегралы вида , где R - рациональная функция, требуют применения универсальной тригонометрической подстановки . При этом используются следующие формулы:

; .

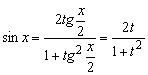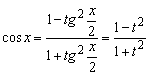В результате преобразования подынтегрального выражения получаем интеграл от рациональной функции.