Интегрирование некоторых функций,

содержащих квадратный трехчлен

Интеграл находится путем выделения полного квадрата из квадратного трехчлена, стоящего в знаменателе. В результате получается табличный интеграл или .

Интеграл аналогичными действиями сводится к табличным или .

Для нахождения интеграла необходимо выделить в числителе дроби дифференциал знаменателя и разложить полученный интеграл на сумму двух интегралов: первый из них сводится к виду где , а второй интеграл вида .

Для нахождения интеграла следует также в числителе дроби выделить дифференциал подкоренного выражения и разложить интеграл на сумму двух: первый сводится к интегралу от степенной функции вида 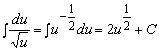, где , а второй интеграл - это интеграл вида .