Непосредственное интегрирование

Таблица интегралов

Пример 1. Найти .

Решение. Представим подынтегральную функцию в виде суммы простых функций, используя формулу квадрата разности:

Были использованы свойства неопределенного интеграла, формулы таблицы интегралов. Произвольные постоянные, получающиеся после интегрирования каждого слагаемого, объединены в одну постоянную С, так как сумма постоянных есть так же постоянная.

Пример 2. Найти

Решение. Разделим почленно числитель на знаменатель, в результате получим сумму двух степенных функций, каждую из которых проинтегрируем:

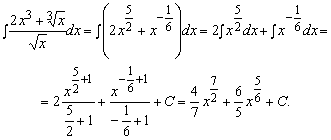
Пример 3. Найти

Решение. Если применить формулу , интеграл сводится к сумме табличных интегралов:

Пример 4. Найти .

Решение. Под знаком интеграла стоит неправильная дробь, а выделяя целую часть, получим

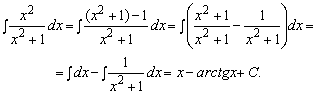
Пример 5. Найти .

Решение. Данный интеграл станет табличным, если под знаком дифференциала будет аргумент подынтегральной функции 5х. Так как d(5x)=5dx, то для создания необходимого дифференциала нужно ввести уравнивающий постоянный множитель , который можно записать перед интегралом. Получим , это табличный интеграл, вида в котором переменная интегрирования u = 5x.

Пример 6. Найти .

Решение. Из выражения, стоящего в числителе, можно создать дифференциал знаменателя . Тогда , получен табличный интеграл , где переменная интегрирования . Перед интегралом стоит уравнивающий множитель –. Получаем

Пример 7. Найти .

Решение. Данный интеграл можно записать в виде . Заметим, что , тогда сведем исходный интеграл к табличному интегралу от степенной функции , где переменная интегрирования . Итак, имеем

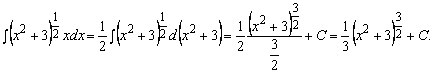
Пример 8. Найти .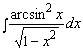

Решение. Известно, что производная функции равна дроби , тогда дифференциал . Следовательно, искомый интеграл можно представить в виде табличного интеграла , где , тогда

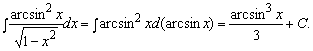
Пример 9. Найти

Решение. Так как , . Получаем табличный интеграл , где .

Пример 10. Найти .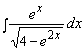

Решение. Представим числитель , следовательно, данный интеграл сводится к табличному интегралу :

.
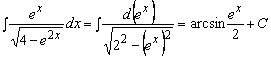