Исследование и построение графиков функций

Исследование и построение графиков функций целесообразно выполнять по следующему алгоритму.

1. Найти область определения функции.

2. Выяснить, является ли функция четной или нечетной, периодической.

3. Определить непрерывность функции, точки разрыва.

4. Найти точки пересечения графика функции с осями координат.

5. Определить интервалы возрастания и убывания функции.

6. Найти точки экстремума функции и вычислить значение функции в этих точках.

7. Определить интервалы выпуклости и вогнутости функции.

8. Найти точки перегиба.

9. Найти асимптоты.

10. Построить график функции.

Рассмотрим более подробно некоторые вопросы исследования функций.

Определение интервалов

возрастания и убывания функций

Определение 1.Функция называется возрастающей (убывающей) в интервале , если для любых двух чисел x₁ и x₂ из этого интервала, где , выполняется неравенство

.

На рис. 1 представлен график возрастающей функции, на рис. 2 - убывающей.

Возрастание и убывание функции характеризуется знаком ее производной : если дифференцируемая в интервале функция имеет , то она возрастает, если , то функция убывает в этом интервале.

Рис. 1 Рис. 2

Нахождение точек экстремума функции

Определение 2. Функция имеет в точке x = x₀ максимум f(x₀), если существует окрестность этой точки (при ), в которой выполняется неравенство . Данная функция в точке x = x₀ имеет минимум f(x₀), если существует окрестность этой точки (при ), в которой выполняется неравенство .

Точки максимума и минимума функции называются точками экстремума функции, а значение функции в этих точках - максимумом и минимумом функции, или экстремумами функции.

Укажем необходимое условие существования экстремума функции.

Если функция в точке имеет экстремум и в этой точке существует конечная производная, то она равна нулю. Точки, в которых производная равна нулю, или обращается в бесконечность, или не существует, называют критическими. Указанное условие экстремума является необходимым, но недостаточным. Поэтому, определив критические точки, надо исследовать их на основании достаточных условий существования экстремума. Существует два таких условия.

Первое достаточное условие экстремума: пусть - критическая точка непрерывной функции . В некоторой окрестности точки , т.е. в интервале , как слева от точки , так и справа существует (по крайней мере, при ) конечная производная, которая сохраняет знак справа и слева от точки . Если при переходе (слева направо) через критическую точку производная меняет знак с плюса на минус, то в точке функция имеет максимум; если с минуса на плюс, то минимум; если производная знака не меняет, то экстремума нет.

Второе достаточное условие существования экстремума: пусть - точка, в которой и существует вторая производная в этой точке, тогда если , то в точке функция имеет максимум; если , то в функция имеет минимум; если , то вопрос о существовании экстремума остается открытым и для его решения необходимо провести исследование по первому условию.

Нахождение интервалов выпуклости,

вогнутости графика функции и точек перегиба

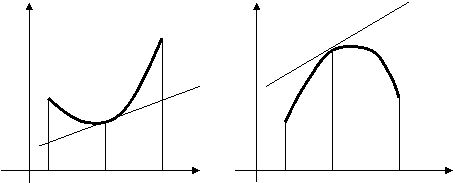
Определение 3. Кривая является вогнутой (выпуклой) на интервале , если все точки кривой лежат выше (ниже) любой ее касательной на этом интервале (рис. 3, 4).

Y Y

O а х₀ b X O a x₀ b X

рис. 3 рис. 4

Определение 4. Точкой перегиба графика непрерывной функции называется точка, при переходе через которую кривая меняет направление вогнутости. Абсциссы точек кривой, в которых вторая производная функции не существует или равна нулю, называются критическими точками второго рода.

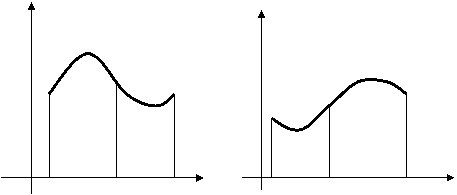
Укажем достаточное условие существования точки перегиба. Пусть точка - критическая точка второго рода функции . В окрестности этой точки функция имеет вторую производную, кроме, быть может, самой точки . Тогда если при переходе через критическую точку второго рода вторая производная меняет знак, то точка с абсциссой есть точка перегиба кривой (рис. 5, 6).

Y Y

O а х₀ b X O а х₀ b X

Рис. 5 Рис. 6

Нахождение асимптот графика функции

Определение 5. Прямая называется асимптотой графика функции , если расстояние от произвольной точки , лежащей на кривой, до этой прямой стремится к нулю при бесконечном удалении точки М от начала координат (рис.7). Различают три типа асимптот: горизонтальные, вертикальные и наклонные.

Y

Асимптота

O X

Рис. 7

1. Горизонтальные асимптоты (асимптоты, параллельные оси абсцисс). Для нахождения горизонтальных асимптот надо найти пределы функции при и . Если существуют конечные пределы или , то прямая является горизонтальной асимптотой.

Если не имеет конечного предела ни при , ни при , то функция не имеет горизонтальных асимптот.

2. Вертикальные асимптоты (асимптоты, параллельные оси ординат) следует искать в точках разрыва функции. Если точка является точкой разрыва, то находят односторонние пределы функции в этой точке. Если хотя бы один из пределов обращается в бесконечность, то прямая является вертикальной асимптотой графика функции.

3. Наклонные асимптоты. Для нахождения наклонных асимптот графика функции надо найти значения параметров и :

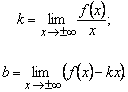
Наклонные асимптоты существуют, когда эти пределы конечны. Если , то наклонная асимптота становится горизонтальной.