Примеры на исследование

и построение графиков функций

 

Пример 1. Исследовать функцию .

Решение.

1. Функция определена и непрерывна на всей числовой оси.

2. Для того чтобы выяснить, является ли функция четной, необходимо проверить, выполняется ли равенство . Для нечетной функции должно выполняться условие .

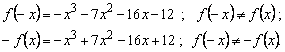
Функция не является ни четной, ни нечетной.

3. Найдем точки пересечения графика функции с осью  при :

Разложим многочлен на множители, получим

График функции пересекает ось  в точках (2, 0) и (3, 0).

Найдем точки пересечения графика функции с осью . При  .

График функции пересекает ось  в точке (0, –12).

4. Производная функции: .

Решая уравнения , получим критические точки

Расположим критические точки на оси абсцисс в порядке возрастания и исследуем знак производной в окрестности каждой критической точки (рис. 1).

 


                +                                         -                                  +

                          2                                                                                         X

Рис. 1

На интервалах  функция возрастает, так как  На интервале  функция убывает, так как .

5. При переходе через критическую точку  производная меняет знак с минуса на плюс. Следовательно, в этой точке функция имеет минимум. В точке  функция имеет максимум. Значения функции в точках экстремума:

.

6. Вторая производная функции: . Решая уравнение , находим критическую точку второго рода:

.

Расположим полученную критическую точку на числовой оси и исследуем знак производной в окрестности этой точки (рис. 2).

 

 


                                      -                                                             +

                                                                                                                             X

Рис. 2

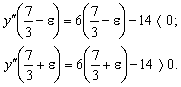
На интервале  график функции выпуклый, так как . На интервале график функции вогнутый, так как .

7. При переходе через критическую точку второго рода  вторая производная функции меняет знак. Следовательно, на основании достаточного условия существования точки перегиба точка  является точкой перегиба графика функции.

.

8. Найдем асимптоты графика функции.

.

Горизонтальных асимптот нет.

Так как функция определена и непрерывна на всей числовой оси, вертикальных асимптот нет:

.

Наклонных асимптот функция не имеет.

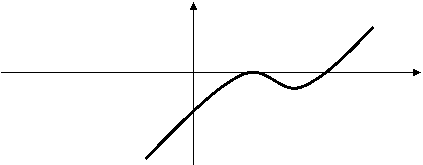
9. Построим график функции  (рис. 3).

 

         Y

 

 

                                                                           2                   3

 

                                                                O                                                                      X

 

                                                                      - 12

 

 

Рис. 3

Пример 2. Исследовать функцию и построить ее график

.

Решение.

1.         Данная функция определена и непрерывна на всей числовой оси за исключением точки .

2.         Функция не является ни четной ни нечетной.

3.         Функция пересекает оси координат в точке .

4.         Первая производная функции:

.

Решая уравнение  находим критические точки

.

Расположим их на числовой оси и исследуем знак производной в окрестности каждой из этих точек (рис. 4).

 


       +                                             -                              -                              +

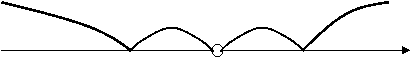
                                             - 2                       -1                       0                               X

 

Рис. 4

 

;

;

;

.

С учетом того что в точке  функция не определена, получим: на интервалах  функция возрастает, на интервалах  убывает.

5. При переходе через критическую точку  производная меняет знак с плюса на минус. Следовательно, в этой точке функция имеет максимум. При переходе через критическую точку  производная меняет знак с минуса на плюс. Следовательно, в этой точке минимум.

Найдем значения функции в точках экстремума:

.

6. Находим вторую производную функции:

.

Вторая производная не обращается в нуль, а при  функция не определена. Следовательно, критических точек второго рода функция не имеет.

Исследуем знак второй производной (рис. 3.15).

 

 


                                      -                                                             +

 


                                                                      - 1                                                                               X

Рис. 5

 

На интервале  график функции выпуклый, на интервале  вогнутый.

7. Так как функция критических точек второго рода не имеет, точки перегиба графика функции отсутствуют.

8. Найдем асимптоты графика функции.

.

Горизонтальных асимптот нет. Для нахождения вертикальных асимптот считаем односторонние пределы , . Следовательно, прямая - вертикальная асимптота.

Ищем наклонные асимптоты.

;

.

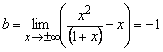Следовательно, прямая  является наклонной асимптотой графика функции.

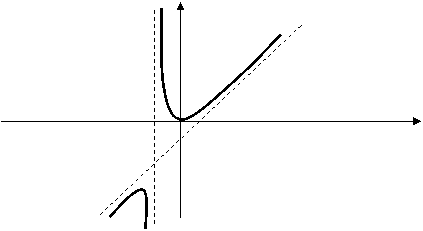
8.       Построим график функции  (рис. 3.16).

 

 

 

 


                                                            Y

 

 

 

 

 

 

 

                                               - 1      O          1                                                                                 X

                                                                      - 1

 

 

 

 

 

Рис. 6

Пример 3. Исследовать функцию и построить ее график

.

Решение.

1. Функция определена и непрерывна на интервале .

2. Вопросы о четности и нечетности функции не рассматриваем.

3. При . График функции пересекает ось  в точке .

4. Производная функции:

.

Решая уравнение , получим , критической точкой будет . Исследуем знак производной в окрестности этой точки (рис. 7).

 

 


                                          +                             -

 


                         0                           е                                                                               X

Рис. 7

;

.

На интервале  функция возрастает, на интервале  убывает.

5. При переходе через критическую точку  слева направо производная меняет знак с плюса на минус.

Следовательно, в этой точке функция имеет максимум, причем

.

6. Находим вторую производную:

.

Решая уравнение , получим

.

Исследуем знак второй производной в окрестности этой точки
(рис. 8).

 

 


                                                      -                              +

 

  0                                                                             X

 

Рис. 8

;

.

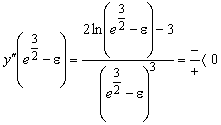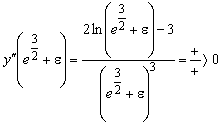На интервале  график функции выпуклый, на интервале 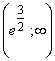- вогнутый.

7. При переходе через критическую точку второго рода  вторая производная меняет знак. Следовательно, точка  является точкой перегиба. Значение функции в этой точке:

.

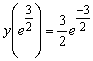8. Найдем асимптоты графика функции.

.

Прямая  является горизонтальной асимптотой.

.

Прямая  является вертикальной асимптотой.

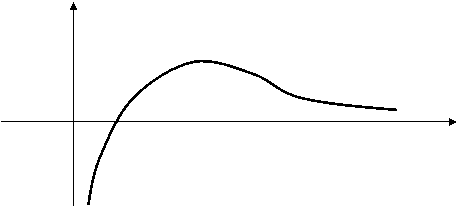
9. Построим график функции  (рис. 9).

 

 

 

 

          Y

 

 

 

 

 

 

          O       1                                е                                                                                 X

 

 

 

 

 

Рис. 9