Дифференциал функции

Дифференциалом функции называется главная линейная относительно часть приращения функции:

.

Так как дифференциал dx независимой переменной x равен приращению этой переменной, то

.

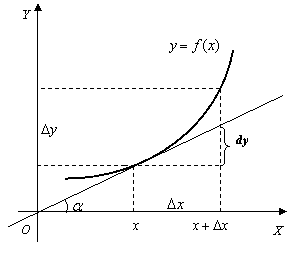
Геометрически дифференциал функции в данной точке представляет собой приращение ординаты касательной, проведенной к графику функции в данной точке, когда x получает приращение (рис. 2.1):

.

Важным свойством дифференциала функции является инвариантность его формы: формула дифференциала не изменится, если вместо функции (от независимой переменной x) рассматривать функцию от зависимой переменной :

.

Другие свойства дифференциала аналогичны свойствам производной:

1) ; 4) ;

2) ; 5) .

3) ;