Гипербола

Гиперболой называется геометрическое место точек плоскости, модуль разности расстояний от которых до двух данных точек и , называемых фокусами гиперболы, есть величина постоянная (не равная нулю и меньшая, чем расстояние между фокусами).

Если обозначить постоянную величину через 2а, а расстояние между фокусами через 2с и выбрать систему координат так, чтобы ось OX проходила через фокусы, а начало координат совпадало с серединой отрезка (рис. 1), то уравнение гиперболы примет канонический вид:

,

где ; и .

Оси координат являются осями симметрии гиперболы, а точка О - ее центром симметрии, а и b - действительная и мнимая полуоси. Точки пересечения гиперболы с действительной осью называются действительными вершинами и . Точки и - мнимыми вершинами.

Прямые являются асимптотами гиперболы.

Эксцентриситет гиперболы .

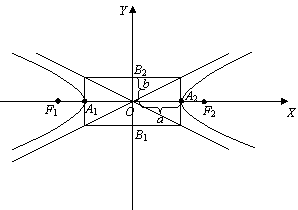
Рис. 1

Уравнение гиперболы с осями, параллельными координатным осям, имеет вид

,

где - координаты центра симметрии.

Если оси гиперболы равны, т.е. а = b, то гипербола называется равносторонней. Ее уравнение .

Для равносторонней гиперболы основной прямоугольник превращается в квадрат, а эксцентриситет равен .