Эллипс
Эллипсом называется геометрическое место
точек плоскости, сумма расстояний от которых до двух данных точек 
и 
, называемых фокусами, есть величина постоянная (большая, чем
расстояние между фокусами).
Если обозначить расстояние между фокусами
через 2с, а сумму расстояний через 2а и выбрать систему координат так,
чтобы ось 
проходила через
фокусы, а начало координат совпадало с серединой отрезка 
(рис. 1), то уравнение
эллипса примет канонический вид
,
где 
; 
и 
.
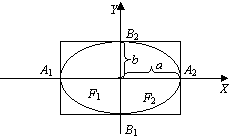
Рис. 1
Оси координат являются осями симметрии
эллипса, точка О - центр симметрии. Точки пересечения
эллипса с осями симметрии называются вершинами эллипса, а - большая полуось эллипса, b -
малая полуось.
Величина 
называется
эксцентриситетом эллипса. Эксцентриситет характеризует форму эллипса.
Если a = b, с = 0 и 
= 0, то это
окружность, фокусы слились в одной точке - центре окружности.
.
Уравнение эллипса с осями симметрии,
параллельными осям координат, имеет вид
,
где 
- координаты центра
симметрии эллипса.