Уравнение плоскости в пространстве

Уравнение плоскости в пространстве имеет вид

Ax+By+Cz+D = 0, где (A; B;C) - вектор, перпендикулярный плоскости.

Уравнение плоскости в координатных отрезках:

,

где a, b и с - отрезки, отсекаемые плоскостью на осях координат.

Расстояние точки М от плоскости Ax+By+Cz+D = 0 вычисляется по формуле

.

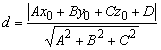
Если даны две плоскости и , то условие их параллельности

.

Условие перпендикулярности плоскостей:

.

Угол между двумя плоскостями определяется формулой:

.

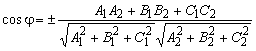Нормальное уравнение плоскости:

,

где - длина перпендикуляра, опущенного из начала координат на плоскость; - направляющие косинусы этого перпендикуляра.

Уравнение плоскости, проходящей через точку с нормальным вектором (А; В; С) имеет вид

.

Уравнение плоскости, проходящей через три точки, и , имеет следующий вид:

.
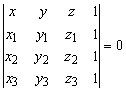