Прямая и плоскость

Даны канонические уравнения прямой

Пример. Найти проекцию точки А(2; –1; 3) на плоскость x + 2y – z – 3 =0.

Решение. Проекцию точки А на плоскость найдем как точку пересечения плоскости перпендикуляром, опущенным из точки А на данную плоскость. Составим уравнение перпендикуляра, опущенного из точки А(2; –1; 3) на плоскость x + 2y – z – 3 = 0:

Из условия перпендикулярности прямой и плоскости имеем ,

т.е. m = 1, n = 2, p = –1. Уравнения перпендикуляра примут вид

.

Чтобы найти точку пересечения прямой и плоскости, нужно решить систему из уравнений прямой и плоскости:

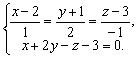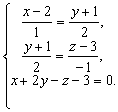или или

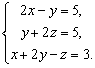
Решая указанную систему, получим координаты проекции точки А на данную плоскость: (3; 1; 2).