Предел функции

Пусть функция определена в некоторой окрестности точки за исключением, быть может, точки .

Число А называется пределом функции в точке (или при ), если для любого сколь угодно малого положительного числа найдется такое число , что для всех , удовлетворяющих условию , выполняется неравенство . Обозначение:

.

Если в определении предела рассматривать только , то имеем понятие левого (правого) предела функции в точке , который обозначается так:

; .

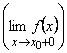Число А называется пределом функции при , если для любого сколь угодно малого положительного числа найдется такое число , что для всех , удовлетворяющих условию , выполняется неравенство . Обозначение:

.

Аналогично определяется предел функции при . Для конечного числа функций, имеющих пределы, выполняются теоремы о пределах:

1)

;

2) ;

( c = const);

3) 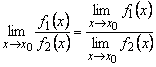, если .

Функция называется бесконечно малой при , если ее предел равен 0.

Алгебраическая сумма (произведение) конечного числа бесконечно малых функций есть функция бесконечно малая.

Произведение бесконечно малой функции и ограниченной - функция бесконечно малая.

Функция называется бесконечно большой при , если предел ее модуля в этой точке равен :

.

Аналогично определяются бесконечно большие функции при . Произведение бесконечно больших функций - функция бесконечно большая. Связь между бесконечно большими и бесконечно малыми функциями следующая: если - бесконечно малая функция при , то - бесконечно большая функция при ; если - бесконечно большая функция при , то - бесконечно малая функция при .

При нахождении предела , когда и - бесконечно малые функции (бесконечно большие функции) при , принято говорить, что отношение при представляет собой неопределенность вида . Аналогично рассматриваются неопределенности вида .