Семинар 14. Нелинейное программирование.

Задачи нелинейного программирования, содержащие две переменные, можно решать графическим методом. Основные принципы решения те же, что и в линейном программировании.

Алгоритм графического метода

1. Построить область допустимых решений.

2. Построить семейство линий уровня, проходящих через область допустимых решений.

3. Построить вектор-градиент целевой функции, который определяет направление возрастания (убывания) функции.

4. Выбрать линию уровня, наиболее удаленную в направлении вектора-градиента (или в противоположном направлении - в задаче на минимум) и проходящую через область допустимых решений. Определить точки области, через которые она проходит.

5. Найти координаты точек экстремума и значение целевой функции в этих точках.

Пример 1. Найти глобальные экстремумы функции при ограничениях

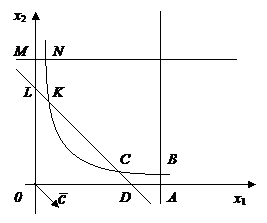
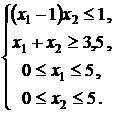
Решение. Построим область допустимых решений. Она состоит из двух частей: и . Линиями уровня являются параллельные прямые . Градиент функции . Следовательно, функция достигает своего глобального максимума в точке , , а в точке - глобального минимума, . Очевидно, что в точке функция имеет локальный минимум, а в точке - локальный максимум.

Пример 2. Найти глобальные экстремумы функции

при ограничениях

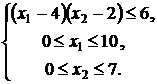
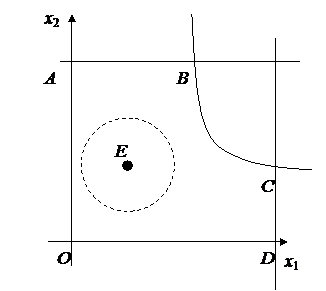
Решение.

Множество является областью допустимых решений. Линии уровня функции z представляют собой концентрические окружности с центром в точке Е и радиусом . Из чертежа видно, что максимум достигается в точке и , мини-

мум – в точке Е, .

Пример 3. Определить глобальный минимум функции на множестве решений системы

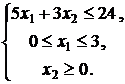
Решение.

Множество допустимых решений является выпуклым. Линии уровня функции z – эллипсы с центром в точке . Минимум достигается в точке касания прямой и некоторого эллипса из семейства линий уровня. Из уравнения прямой определим ее вектор нормали . В точке касания градиент функции направлен по нормали к линии уровня, то есть его направление совпадает с направлением нормали к прямой . Найдем градиент функции

.

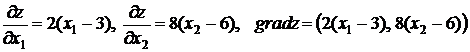Так как точка касания лежит на прямой и в ней градиент функции коллинеарен вектору нормали к прямой , то получаем систему из двух уравнений для определения координат этой точки:

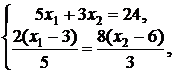или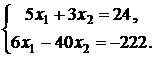

Решением данной системы является:

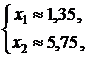
откуда , при этом .

Пример 4. Найти экстремумы функции при условии

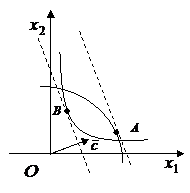
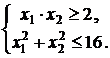
Решение. Из рисунка видно, что минимум целевой функции достигается в точке , а максимум в точке .

Точка В является точкой пересечения линии уровня , и гиперболы .Найдем ее координаты.

.

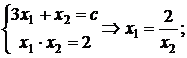
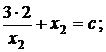
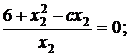
Так как точка касания линии уровня и гиперболы должна быть единственной, у этого уравнения должен быть единственный корень.

, тогда . Таким образом,

.

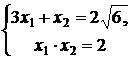
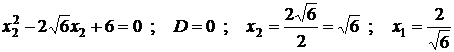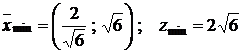
Точка А есть пересечение линии уровня и прямой ОА. Угловой коэффициент линии уровня: . Поскольку касательная и радиус, проведенный к точке касания, перпендикулярны, Тогда уравнение прямой ОА: . Найдем координаты точки А.

, .

.

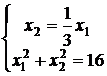
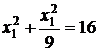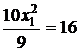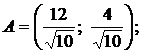
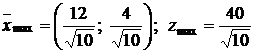Задачи

1. Определить глобальный максимум функции при условиях

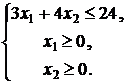
2. Найти глобальные экстремумы функции на множестве решений:

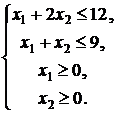
3. Найти максимальное и минимальное значения функции при ограничениях

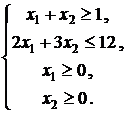
4. Найти наибольшее значение функции при условиях

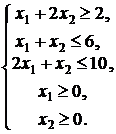
5. Найти глобальные экстремумы функции в области решений системы неравенств:

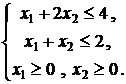
6. Найти глобальный максимум функции при ограничениях

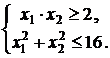
7. В области решений системы неравенств

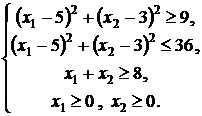
определить глобальные экстремумы следующих функций:

а) ; б) ; в) .

8. Найти наименьшее значение функции при условиях

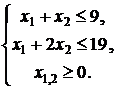
9. Найти глобальный максимум функции при ограничениях

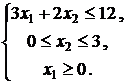
10. В области решений системы линейных неравенств

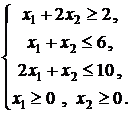
найти наименьшее и наибольшее значения следующих целевых функций:

а) ; б) .

Ответы

1. .

2. , .

3. , .

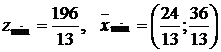4. .

5. , .

6. , .

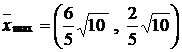7. а) , .

б) ; возможны альтернативные решения

.

в) ,

.

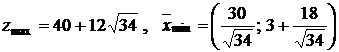8. .

9. .

10. а) ,

б) или ;

.