Семинар 10. Теория двойственности

Каждой задаче линейного программирования можно поставить в соответствие другую задачу, называемую двойственной по отношению к исходной.

В зависимости от вида исходной задачи различают симметричные, несимметричные и смешанные пары двойственных задач.

Пара двойственных задач называется симметричной, если одна из задач задана в симметричном виде.

Перед началом составления двойственной задачи в исходной задаче знаки неравенств системы ограничений приводят к единому виду: «» в задаче на максимум, «» в задаче на минимум.

Пусть исходная задача линейного программирования имеет вид:

,

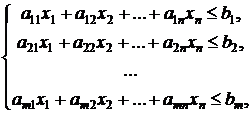
Правило составления двойственных задач. Симметричная пара

1. Каждому ограничению исходной задачи ставится в соответствие двойственная переменная y_i, где .

2. Составляется целевая функция , коэффициентами которой будут свободные члены системы ограничений исходной задачи, а цель задачи меняется на противоположную:

.

3. Составляется система ограничений двойственной задачи. Матрицу коэффициентов системы ограничений двойственной задачи получают из матрицы коэффициентов исходной задачи путем транспонирования. Знаки неравенств системы ограничений двойственной задачи противоположны знакам неравенств в исходной задаче. Свободными членами неравенств системы ограничений являются коэффициенты целевой функции исходной задачи. Переменные y_i в двойственной задаче также неотрицательны.

Итак, двойственная задача состоит в нахождении наименьшего значения функции

при ограничениях:

.

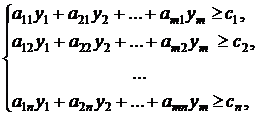
Если двойственную задачу принять за исходную, поставить в соответствие каждому неравенству системы ограничений переменную х_j, и по данному выше правилу составить двойственную задачу, то получим исходную задачу. Понятие двойственности является взаимным.

Правило составления двойственных задач. Несимметричная пара

Пара двойственных задач называется несимметричной, если одна из задач имеет канонический вид и переменные неотрицательны или одна из задач задана в неканоническом виде и переменные произвольны по знаку.

Если в системе ограничений исходной задачи – уравнения, то соответствующие им двойственные переменные произвольны по знаку. Если переменные исходной задачи неотрицательны, то ограничения двойственной задачи имеют вид неравенств со знаком «³», если задача решается на минимум, и «£», если на максимум. Далее построение двойственной задачи осуществляют так же, как для симметричной пары.

Пусть исходная задача имеет вид:

,

при ограничениях:

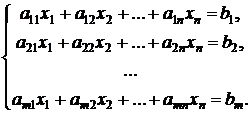
Двойственная задача состоит в нахождении наименьшего значения функции:

при ограничениях:

.

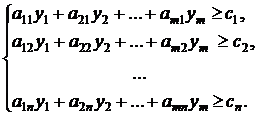
Пусть исходная задача имеет вид:

,

при ограничениях:

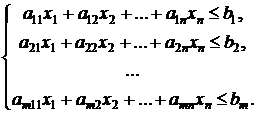
Тогда двойственная задача имеет вид:

при ограничениях:

.

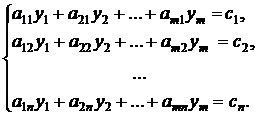
Правило составления двойственных задач. Смешанная пара

Когда система ограничений одной из задач содержит как уравнения, так и неравенства, и некоторые переменные неотрицательны, пара двойственных задач называется смешанной.

При построении двойственной задачи в смешанной паре придерживаются следующего правила. Если двойственная переменная поставлена в соответствие ограничению-неравенству, то она неотрицательна, если уравнению - то произвольна по знаку. Если исходная переменная неотрицательна, ей ставится в соответствие ограничение- неравенство; если переменная произвольна по знаку –соответствующее ей ограничение – уравнение. Далее используют то же правило, что и для симметричной пары.

Пусть исходная задача имеет вид:

при ограничениях:

.

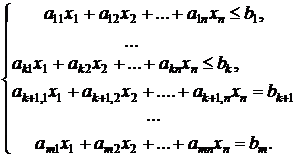
Тогда двойственная задача имеет вид:

при ограничениях:

,

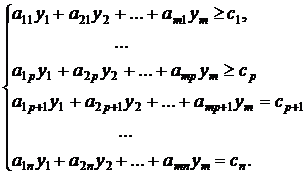
Пример 1. Составить двойственную задачу к следующей: найти наибольшее значение функции

при ограничениях:

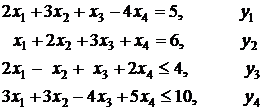
х₁ ³ 0, х₂ ³ 0, х₃ и х₄ свободны по знаку.

Двойственная задача: найти наименьшее значение функции

при ограничениях:

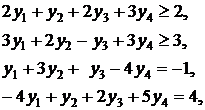
y₁, y₂ свободны по знаку, у₃ ³ 0, у₄ ³ 0.

Нахождение решения двойственных задач

Первый способ нахождения решения двойственной задачи в симметричной паре основан на применении основных теорем двойственности.

Первая теорема двойственности: если одна из двойственных задач имеет оптимальное решение, то и другая имеет оптимальное решение, причем для оптимальных решений и выполняется равенство:

.

Если целевая функция одной из задач не ограничена на ОДР, то система ограничений двойственной задачи не совместна, и наоборот.

Следствие из второй теоремы двойственности: если на оптимальном решении одной из двойственных задач какое-либо ограничение этой задачи выполняется как строгое неравенство, то соответствующая переменная в оптимальном решении другой задачи равна нулю. Если в оптимальном решении одной из двойственных задач какая-либо переменная положительна, то соответствующее ей ограничение в другой задаче на оптимальном решении выполняется как равенство.

Пример 2. Дана задача линейного программирования в неканоническом виде

,

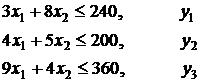
х₁ ³ 0 , х₂ ³ 0.

Данная задача имеет оптимальное решение

Составим двойственную задачу:

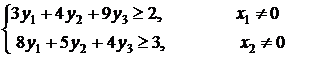
у_i ³ 0, .

Из первой теоремы двойственности следует, что .

Применим вторую теорему двойственности: так как в оптимальном решении исходной задачи и , то на оптимальном решении двойственной задачи первое и второе ограничения двойственной задачи выполняются как равенства

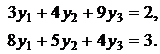
Подставим в ограничения исходной задачи и получим, что третье ограничение выполняется как строгое неравенство:

9 × 23,53 + 4 × 21,18 = 296,49, т.е. 296,49<360 Þ у₃ = 0.

Получим систему трех уравнений с тремя неизвестными:

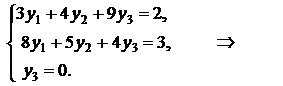
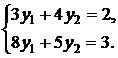
Решая систему, получим .

Второй способ нахождения решения двойственной задачи в симметричной паре основан на использовании симплексного метода.

Если одна из двойственных задач решена симплексным методом, то оптимальное решение двойственной задачи можно найти из оценочной строки последней итерации. Для этого нужно установить соответствие между основными переменными одной задачи и балансовыми переменными двойственной задачи.

Запишем системы ограничений симметричной пары двойственных задач:

.

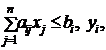
Приведем их к каноническому виду:

,

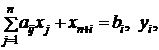
где x₁, x₂, …, x_n - основные, x_n+1, x_n+2, …, x_n+m - балансовые;

y_m+1, y_m+2, …, y_m+n - балансовые, y₁, y₂, …, y_m - основные.

Если исходная задача решена симплексным методом, то

,

где - симплексные оценки переменных исходной задачи.

Если двойственная задача решена симплексным методом, то

,

где - симплексные оценки переменных двойственной задачи.

Пример 3. Найти наименьшее значение функции

при ограничениях:

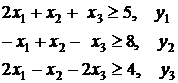
х_i ³ 0, .

Решение. Составим двойственную задачу:

,

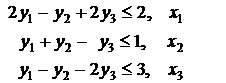
у_i ³ 0,

Решим двойственную задачу симплексным методом, для этого приведем ее к каноническому виду

2у₁ - у₂ +2у₃+ у₄ =2,

у₁ + у₂ - у₃ + у₅ =1,

у₁ - у₂ - 2у₃ + у₆ =2,

.

Целевая функция остается без изменения.

сj	Б.п.	5	8	4		0	0	0	bi
		у1	у2	у3	у4		у5	у6
0 0 0	у4 у5 у6	2 1 1	-1 1 -1	2 -1 -2		1 0 0	0 1 0	0 0 1	2 1 3
Dj		-5	-8	-4		0	0	0	0
0 8 0	у4 у2 у6	3 1 2	0 1 0	1 -1 -3		1 0 0	1 1 1	0 0 1	3 1 4
Dj		3	0	-12		0	8	0	8
4 8 0	у3 у2 у6	3 4 11	0 1 0	1 0 0		1 1 3	1 2 4	0 0 1	3 4 13
Dj		39	0	0		12	20	0	44

.

Отбрасывая балансовые переменные, получим оптимальное решение двойственной задачи: .

Тогда по первой теореме двойственности .

Установим связь между балансовыми переменными двойственной задачи и основными переменными исходной задачи:

х₁®у₄, х₂®у₅, х₃®у₆.

Тогда х₁=D₄, х₂=D₅, х₃=D₆, .

Нахождение решения двойственной задачи в несимметричной паре

По решению одной из двойственных задач можно найти оптимальное решение другой.

Пример 4. Найти наибольшее значение функции

при ограничениях:

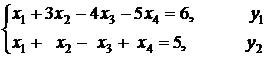
х_i ³ 0, .

Данная задача имеет оптимальное решение

.

Составим двойственную задачу: найти наименьшее значение функции

при ограничениях:

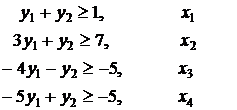
у₁ и у₂ свободны по знаку.

По первой теореме двойственности .

По второй теореме двойственности, так как в оптимальном решении исходной задачи х₂¹0 и х₃¹0, то, выписывая второе и третье ограничения двойственной задачи как уравнения, получим систему из двух уравнений с двумя неизвестными:

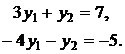
Решая эту систему, получим у₁= -2 и у₂=13, = (-2; 13).

Экономическая интерпретация двойственных задач

Рассмотрим экономическую интерпретацию двойственных задач на примере задачи об оптимальном использовании ресурсов.

Исходная задача: найти наибольшее значение функции

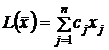
при ограничениях:

,

.

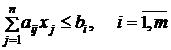Двойственная задача: найти наименьшее значение функции

при ограничениях:

,

.

Установим размерность двойственных переменных y_i, которые еще называют двойственными оценками.

Из ограничений двойственной задачи следует, что размерность произведения a_ij y_i совпадает с размерностью c_j, т.е.
a_ij y_i c_j ( знак означает эквивалентность размерности), отсюда

.

Таким образом, y_i измеряется в рублях на единицу ресурса. Назовем y_i условной ценой или оценкой i-го ресурса.

Рассмотрим свойства оценок.

1) Оценки y_i - мера дефицитности ресурса. Дефицитный ресурс полностью используется при оптимальном плане и имеет положительную оценку, т.е.

.

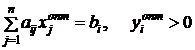Недефицитный ресурс используется не полностью и имеет нулевую оценку, так как если

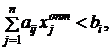то .

2) Оценки y_i - мера влияния свободных членов системы ограничений исходной задачи на значение целевой функции, так как

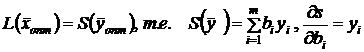
Прирост прибыли пропорционален приращению i-го ресурса, причем коэффициент пропорциональности равен у_i, чем больше у_i, тем эффективнее i-й ресурс.

Пример 5. Рассмотрим задачу определения плана выпуска продукции, дающего наибольшую прибыль

,

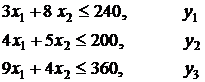
х₁ ³ 0, х₂ ³ 0.

Составим двойственную задачу:

,

.

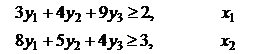
Найдем решения обеих задач:

.

В оптимальном решении двойственной задачи , следовательно, третий вид сырья недефицитный, т.е. при расходуется не полностью. у₁>0 и у₂>0, следовательно, первое и второе сырье дефицитное, и поскольку у₂> у_1, второе сырье оказывает большее влияние на прибыль, есть смысл увеличивать в первую очередь запасы второго сырья.